Java实现模拟小球二维完全弹性斜碰

发表于 | 分类于

Java实现模拟小球二维完全弹性斜碰

QQ的桌球游戏初中那会很流行，当时就想着是怎么做到的呢？游戏开发其中也有很多门道，很多方面。这里我也不懂，只是做了一个桌球游戏的简单实现，实现的过程可能并不完美，不过还是尽量图文并茂、易于理解的写出来。如果有不正确的地方欢迎指正。

功能简述

1、桌面是二维光滑平面，带有边缘（墙壁），没有阻力。
2、球与球之间能实现完全弹性斜碰，即实现真正的物理上桌球的击球效果。

软件架构

绘图使用JFrame嵌套JPanel，JPanel自带双缓冲，能够做到绘图减少闪烁。JPanel内使用Canvas、Graphics、Image绘图，Image也自带双缓冲。
绘图功能由CanvasThread实现，球的运动和计算由CircleThread实现，球的数量控制由ServeThread实现。

png
软件架构

原理详解

注意：在这里的实现中，球和圆是同一个意思，即球可以等价看出圆。

这里的球碰撞主要是要解决两个问题：碰墙、碰球。

球的运动比较简单，球的运动速度矢量V可以分解在xy轴上，即向量Vx和Vy（有方向和大小），单位时间可以通过加上Vx和Vy的改变球的位置坐标Lx、Ly，从而实现球的运动。不过这里有一个小细节需要注意一下，不然会出现球有速度却静止不动的情况。

碰墙比较好解决，只要球超出边界就让它对应的Vx或Vy取反就行，不过这里还有几个小细节需要注意一下，不然会出现球嵌在墙里出不来的情况。

碰球的问题就比较复杂了，高中物理学过一维上两个小球的正面弹性碰撞公式，这里是小球在二维平面上的弹性斜碰情况。（均是光滑、无阻力的平面）

不过弹性斜碰仍然是可以分解转换成正面弹性碰撞的，下面进行分步骤详细解说一下吧。

数据准备：

球内存储的数据为：
img

这些数据共同参与运算构成了整个运行流程。

第零步：先判断两个圆的位置

只有满足两个圆心距离dn小于或等于两个圆的半径和dc的情况才叫碰撞，即两圆相切或相交时，需要做进一步处理。否则两圆相离无需做处理。

相切时的示意图：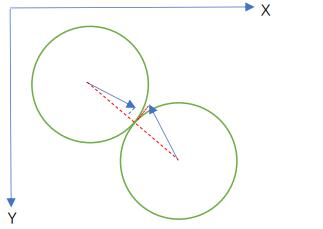
img

第一步：计算合速度的大小和方向

球内存储的数据只有Vx和Vy这两个矢量，没有球运动的合速度矢量。不过解决球的斜碰还是需要合速度矢量的，需要计算出来。

分解速度矢量和合速度矢量：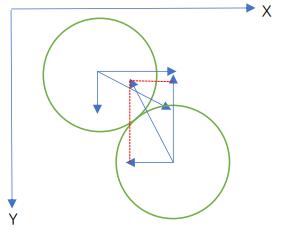
img

第二步：计算共同（相对）坐标系s，解决粘连问题，计算ab在s中的速度的大小和方向

这个步骤比较复杂，需要分成三步来解决。

1）计算共同（相对）坐标系s。

为了将斜碰转化为正碰，需要将球的运动坐标系进行转化，共同坐标系s的x轴是以两个圆心所在直线为基础，因为是球b相对于球a的坐标系，所以坐标系的原点即球a的圆心。

共同（相对）坐标系s：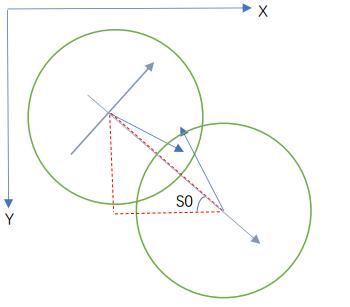
img

2）解决粘连问题，或者碰撞时已经相交的情况，让两个圆后退到相切状态。

让两个圆由相交状态回退到相切状态，需要将两个圆沿着运动方向的反方向移动，移动到相切（或略微有相离）为止。移动的距离就是中间的重叠部分，更详细点就是分别修改圆的x轴和y轴数值，数值大小就是重叠部分的数值，因为是重叠所以要除以2，即 (dn-dc)/2。

移动的加减运算的公式是一致的，这是可以推导的。

解决粘连问题：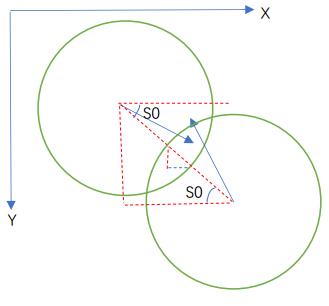
img

3）将ab的速度大小和方向由原坐标系转化为在共同坐标系s中的速度大小和方向。

将ab的合速度投影到共同坐标系s中，便于接下来计算正碰。

坐标转化：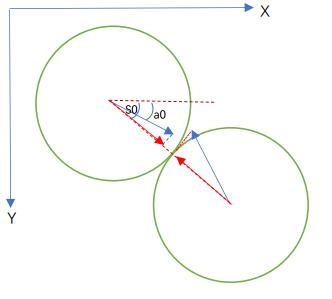
img

第三步：计算完全弹性斜碰

ab球的速度映射到s坐标系后，处在y轴的分速度发生弹性正碰时不受影响。处在x轴的分速度就等价于弹性正碰。

两个小球弹性正碰的公式推导（百度百科）：
img

发生弹性正碰之后，原来的y轴的分速度没有变化，x轴的分速度按公式进行“变换”。

第四步：计算两球发生碰撞后在s中的各自新合速度大小和运动方向

新的合速度和运动方向很容易就可以得出。

发生弹性正碰之后的两个小球的分速度变化和新合速度：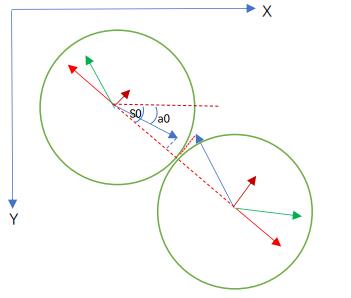
img

第五步：将两球速度转化为原坐标系中的速度

只需要将合速度进行三角运算即可得到映射的分速度。

两球新的合速度矢量转化为原坐标系中的分速度：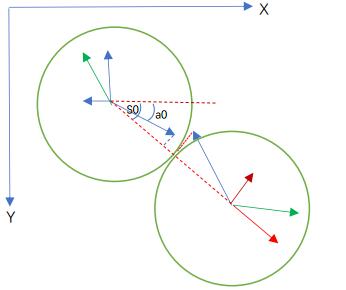
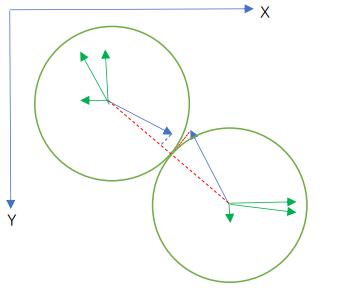
img

img

第六步：更新

将碰撞后的新数据更新到圆的存储中即可。

碰撞后的新方向：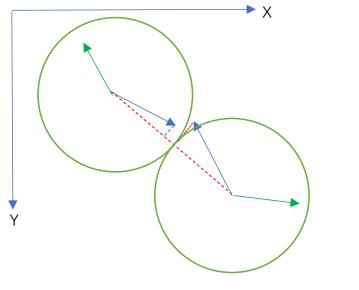
img

补充：整个过程中因为桌面光滑，完全无损失碰撞，所以所有的球的动能和应该是恒定不变的。

关键代码

球的运动和碰墙检测代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
/**
    * 小球沿着vx和vy移动，并对此时移动过程中撞击到墙做判断和处理（先解决球碰墙，再解决球碰球）
    * 
    * 每次移动一个单位的vx和vy
    * 
    * 需要打磨算法才能准确
    */
public void move() {
    // 当X轴上碰到墙时,X轴行进方向改变
    if (lx + vx + radius >= width) {
        // 只有确实是在向右墙运动时才掉头，防止和collide中的调整出现冲突，以下类似
        if (vx > 0)
            vx *= -1;
        else
            // 如果不加这个方法，则球可能会一直嵌在墙里
            moveX();
    } else if (lx + vx - radius <= 0) {
        if (vx < 0)
            vx *= -1;
        else
            moveX();
    }
    // 没碰壁时继续前进
    else {
        moveX();
    }

    // 当在Y轴上碰到墙时,Y轴行进方向改变
    if (ly + vy + radius >= height) {
        if (vy > 0)
            vy *= -1;
        else
            moveY();
    } else if (ly + vy - radius <= 0) {
        if (vy < 0)
            vy *= -1;
        else
            moveY();
    }
    // 没碰壁时继续前进
    else {
        moveY();
    }
}

private void moveX() {
    if (abs(vx) < 1) {
        px += vx;
        if (abs(px) >= 1) {
            lx += round(px);
            px = 0;
        }
    } else {
        lx += vx;
        px = 0;
    }
}

private void moveY() {
    if (abs(vy) < 1) {
        py += vy;
        if (abs(py) >= 1) {
            ly += round(py);
            py = 0;
        }
    } else {
        ly += vy;
        py = 0;
    }
}

球的斜碰：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
/**
    * 解决小球之间的斜碰（二维平面，球==圆）
    * 
    * 坐标系x轴向右为正，y轴向下为正
    * 
    * 需要打磨算法才能准确
    * 
    * @param circle
    */
public void collide(Circle b) {
    Circle a = this;

    int alx = a.lx, aly = a.ly, blx = b.lx, bly = b.ly;
    double avx = a.vx, avy = a.vy, bvx = b.vx, bvy = b.vy;
    int ar = a.radius, br = b.radius;
    int am = a.weight, bm = b.weight;

    // ----- 第零步：先判断两个圆的位置 -----

    double dn = sqrt(pow(alx - blx, 2) + pow(aly - bly, 2));
    double dc = ar + br;
    // 两圆重合
    if (dn == 0)
        return;
    // 两圆相离则返回
    if (dn > dc + Main.ERROR_APART)
        return;

    // ----- 第一步：计算合速度的大小和方向 -----

    // 计算a的合速度的值（不包含方向）
    double av = sqrt(pow(avx, 2) + pow(avy, 2));
    // 计算a的运行角度（运行方向，[-π ~ π)）
    double a0 = acos(avx / av);
    if (avy != 0)
        a0 *= avy / abs(avy);

    // 计算b的合速度的值
    double bv = sqrt(pow(bvx, 2) + pow(bvy, 2));
    // 计算b的运行角度
    double b0 = acos(bvx / bv);
    if (bvy != 0)
        b0 *= bvy / abs(bvy);

    // System.out.println(av + " " + (a0 * 180 / PI));
    // System.out.println(bv + " " + (b0 * 180 / PI));

    // ----- 第二步：计算共同（相对）坐标系s，以及ab在s中的速度的大小和方向 -----

    // ----- 第二步：第一部分：计算共同（相对）坐标系s的参数 -----

    // 计算圆b圆心相对于圆a圆心的坐标（注意y轴为数学上的y轴，与计算机中的y轴相反）
    int sx = blx - alx;
    int sy = bly - aly;

    // 计算b相对于a的速度方向和大小
    double sz = sqrt(pow(sx, 2) + pow(sy, 2));
    double s0 = acos(sx / sz);
    if (sy != 0)
        s0 *= sy / abs(sy);

    // System.out.println(sz + " " + (s0 * 180 / PI));

    // ----- 第二步：第二部分：解决粘连问题，或者检测到碰撞时已经相交，让两个圆分离 -----

    // 在这里 dc-ERROR_CROSS <= dn <= dc+ERROR_APART 算相切

    // 两圆相交（或两圆粘连）
    if (dn < dc - Main.ERROR_CROSS) {
        double de = (dc - dn) / 2;
        double dx = de * cos(s0);
        double dy = de * sin(s0);
        alx -= dx * 2;
        aly -= dy * 2;
        blx += dx * 2;
        bly += dy * 2;
    }

    // ----- 第二步：第三部分：将ab的速度大小和方向由原坐标系转化为在共同坐标系s中的速度大小和方向 -----

    // 在s坐标系中a的新运动方向
    double sa0 = a0 - s0;
    // 在s坐标系中a的新速度大小
    double sav = av;
    // 在s坐标系中a的新速度在s的x轴上的投影
    double savx = sav * cos(sa0);
    // 在s坐标系中a的新速度在s的y轴上的投影
    double savy = sav * sin(sa0);

    // 在s坐标系中b的新运动方向
    double sb0 = b0 - s0;
    // 在s坐标系中b的新速度大小
    double sbv = bv;
    // 在s坐标系中b的新速度在s的x轴上的投影
    double sbvx = sbv * cos(sb0);
    // 在s坐标系中b的新速度在s的y轴上的投影
    double sbvy = sbv * sin(sb0);

    // ----- 第三步：发生完全弹性斜碰时，在s坐标系中，两球y轴速度不变，x轴速度满足完全弹性正碰（由动能定理和动量守恒推导） -----

    // 碰撞后a球s坐标系x轴的分速度
    double savxp = ((am - bm) * savx + 2 * bm * sbvx) / (am + bm);
    // 碰撞后a球s坐标系y轴的分速度
    double savyp = savy;
    // 碰撞后b球s坐标系x轴的分速度
    double sbvxp = ((bm - am) * sbvx + 2 * am * savx) / (am + bm);
    // 碰撞后b球s坐标系y轴的分速度
    double sbvyp = sbvy;

    // ----- 第四步：计算两球发生碰撞后在s中的各自合速度大小和运动方向-----

    // 碰撞后a球在s坐标系的合速度大小
    double savp = sqrt(pow(savxp, 2) + pow(savyp, 2));
    // 碰撞后a球在s坐标系的运动方向
    double sa0p = acos(savxp / savp);
    if (savxp == 0 && savyp == 0)
        sa0p = 0;
    else if (savyp != 0)
        sa0p *= savyp / abs(savyp);
    // 碰撞后b球在s坐标系的合速度大小
    double sbvp = sqrt(pow(sbvxp, 2) + pow(sbvyp, 2));
    // 碰撞后b球在s坐标系的运动方向
    double sb0p = acos(sbvxp / sbvp);
    if (sbvxp == 0 && sbvyp == 0)
        sb0p = 0;
    else if (sbvyp != 0)
        sb0p *= sbvyp / abs(sbvyp);

    // ----- 第五步：将两球速度转化为原坐标系中的速度 -----

    // 碰撞后a球在原坐标系的合速度大小
    double fva = savp;
    // 碰撞后a球在原坐标系的运动方向
    double fa0 = sa0p + s0;
    if (fa0 > PI)
        fa0 -= 2 * PI;
    else if (fa0 <= -PI)
        fa0 += 2 * PI;
    // 碰撞后a球在原坐标系的合速度大小在x轴上的分量
    double fvax = fva * cos(fa0);
    // 碰撞后a球在原坐标系的合速度大小在y轴上的分量
    double fvay = fva * sin(fa0) * -1;

    // 碰撞后b球在原坐标系的合速度大小
    double fvb = sbvp;
    // 碰撞后b球在原坐标系的运动方向
    double fb0 = sb0p + s0;
    if (fb0 > PI)
        fb0 -= 2 * PI;
    else if (fb0 <= -PI)
        fb0 += 2 * PI;
    // 碰撞后b球在原坐标系的合速度大小在x轴上的分量
    double fvbx = fvb * cos(fb0);
    // 碰撞后b球在原坐标系的合速度大小在y轴上的分量
    double fvby = fvb * sin(fb0) * -1;

    // ----- 第六步：更新 -----

    a.lx = alx;
    a.ly = aly;

    b.lx = blx;
    b.ly = bly;

    a.vx = fvax;
    a.vy = fvay;

    b.vx = fvbx;
    b.vy = fvby;
}

测试结果

运行过程中某一个时间段的动图（动图帧率比较低，会显示的有些卡顿）：
img

运行过程中某一刻的球运动数据输出：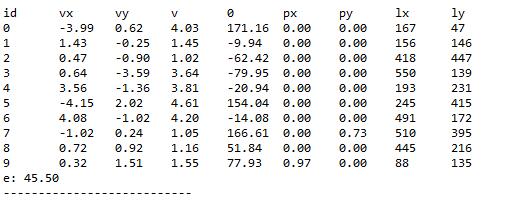
img

从结果可以看出系统总能是守恒的。

总结思考

游戏编程主要是将数学和物理（也有其他学科）的知识结合图像显示出来，编写一些小游戏代码，能够锻炼代码的逻辑能力，也能遇到到一些编程中的细节问题，同时也是将数学转为代码，锻炼思维能力。游戏编写过程中，也能体会到代码加数学的魔性，增强编程的兴趣。

源码

参考博客

csdn