Java多线程之哲学家就餐问题

哲学家就餐问题是在计算机科学中的一个经典问题，常常被用来面试。这个问题显示了多线程同步(Synchronization)时产生的问题。

在1971年，由著名的计算机科学家艾兹格•迪科斯彻提出，即假设有五台计算机都试图访问五份共享的磁带驱动器。不久，为了便于理解和生动化，这个问题又被托尼•霍尔重新表述为哲学家就餐问题。该问题可以用来解释死锁和资源竞争。

操作系统原理之进程和线程管理
 Java的多线程和并发知识纲要
 Java多线程之生产者和消费者模式

问题描述

一张圆桌上坐着5名哲学家，每两个哲学家之间的桌上摆一根筷子，桌子的中间是一碗米饭，如下图所示。哲学家们倾注毕生精力用于思考和进餐，哲学家在思考时，并不影响他人。每个哲学家思考的时间是固定的，不是永久都在思考。只有当哲学家饥饿的时候，才试图拿起左、右两根筷子（一根一根地拿起）。如果筷子已在他人手上，则需等待。这个等待可能是一直等待，也有可能是等待一会就放弃（同时放下手中已有的筷子）。饥饿的哲学家只有同时拿到了两根筷子才可以开始进餐。同样，每个哲学家吃饭的时间是固定的，不是一直都在吃饭。当进餐完毕后，放下筷子继续思考。

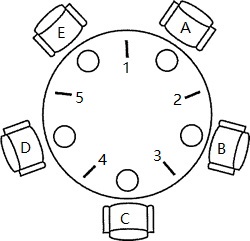
哲学家就餐问题

问题分析

5名哲学家与左右邻居对其中间筷子的访问是互斥关系，可以把哲学家比作五个进程。问题的关键是如何让一个哲学家能吃到饭而不造成死锁或者饥饿现象。

每一个哲学家的状态可以分为：思考（无需筷子）、饥饿（需要筷子）、吃饭（占有两个筷子）。

如果不设计好哲学家的吃饭规则，那么会导致死锁和饥饿。
假设五个哲学家按顺序分别是A，B，C，D，E。

死锁的例子：
大家都同时拿起左边的筷子，然后等待右边的筷子。即A拿到了筷子2，然后等待筷子1；E拿到了1，再等待5；D拿到了5，再等待4；C拿到了4，再等待3；B拿到了3，再等待2；而A一直不放下筷子2。那么就形成了死锁。

饥饿的例子：
基于死锁的例子，不同的是，大家先检查右边的筷子是否可以拿，发现可以，然后都同时拿起左边的筷子，接着又同时去拿右边的筷子，但是发现右边拿不到（相对的），就同时放下了左手的筷子，放下筷子后又发现自己右边的筷子可以拿了，就又同时拿起了左边的筷子。循环往复，那么就形成了饥饿。

在这个问题中，不难发现，最多只有两个哲学家能同时就餐，而正确的情况是每个哲学家都能吃到饭。

我的解决

解决这个问题需要设计正确的吃饭规则，不能想吃就吃。

比如：
1）同时只允许一位哲学家就餐。
2）对哲学家顺序编号，要求奇数号哲学家先抓左边的叉子，然后再抓他右边的叉子；而偶数号哲学家刚好相反，先抓右边的叉子，然后再抓他左边的叉子。
3）当且仅当某一个哲学家他的左右两边的叉子都可用时，才允许抓起叉子。

做法一可行但是效率低，本来可以最多两个哲学家吃饭，现在只能是一个。
做法二可行，不过需要对哲学家分类，也就是进程分类，操作比较麻烦，需要制定两套方案。
做法三也是可行的，同时也是不错的解决方法，每个哲学家都是平等的。

PV操作模型可以直观的表示这些方法，不过落实到具体的代码上就不是模型表现的那么简单了，好在JavaAPI已经提供了相关的类或方法可以直接使用。

公共类和方法

抽象的筷子类：

package com.chain.test.day04;

/**
 * 筷子的抽象类
 * 
 * 临界资源，只能同时被一个哲学家使用（抓起）
 * 
 * @author chain
 *
 */
public abstract class AbstractChopstick {

	// 筷子序号
	protected int id;

	public AbstractChopstick(int id) {
		this.id = id;
	}

	/**
	 * 获得筷子序号
	 * 
	 * @return
	 */
	public int getId() {
		return id;
	}

	/**
	 * 获得筷子名字
	 * 
	 * @return
	 */
	public String getName() {
		return "Chopstick-" + getId();
	}

	/**
	 * 筷子是否被使用
	 * 
	 * @return
	 */
	public abstract boolean isUse();

	/**
	 * 使用（抓起）筷子
	 * 
	 * @throws Exception
	 */
	public abstract void use() throws Exception;

	/**
	 * 放下筷子
	 */
	public abstract void drop();

}

哲学家抽象类：

package com.chain.test.day04;

/**
 * 哲学家抽象类
 * 
 * @author chain
 *
 */
public abstract class AbstractPhilosopher {

	// 哲学家序号
	protected int id;

	public AbstractPhilosopher(int id) {
		this.id = id;
	}

	/**
	 * 获得哲学家的序号
	 * 
	 * @return
	 */
	public int getId() {
		return id;
	}

	/**
	 * 获得哲学家的名字
	 * 
	 * @return
	 */
	public String getName() {
		return "Philosopher-" + getId();
	}

	/**
	 * 思考
	 * 
	 * @throws Exception
	 */
	public abstract void think() throws Exception;

	/**
	 * 抓筷子
	 * 
	 * @throws Exception
	 */
	public abstract void take(AbstractChopstick chopstick) throws Exception;

	/**
	 * 放筷子
	 */
	public abstract void put(AbstractChopstick chopstick);

	/**
	 * 就餐
	 * 
	 * @throws Exception
	 */
	public abstract void eat() throws Exception;

}

哲学家就餐的方法的抽象类：

package com.chain.test.day04;

/**
 * 哲学家抓放筷子的方法的抽象类
 * 
 * @author chain
 *
 */
public abstract class AbstractPhilosopherMethod {

	/**
	 * 哲学家
	 * 
	 * 吃饭在前，思考在后
	 * 
	 * @throws Exception
	 */
	public abstract void method(Philosopher p, AbstractChopstick[] cs) throws Exception;
}

测试方法、Philosopher、Chopstick的具体实现可以文章底部源码连接中可以查阅到。

对于Chopstick这个临界资源，实现PV操作的方式有多种。

先拿起左叉子，再拿起右叉子

test.properties：

1
2
3

chopstick.class=com.chain.test.day04.Chopstick01
philosopher.class=com.chain.test.day04.Philosopher
philosopher.method.class=com.chain.test.day04.PhilosopherMethod01

package com.chain.test.day04;

/**
 * 每个哲学家先拿起左叉子，再拿起右叉子
 * 
 * @author chain
 *
 */
public class PhilosopherMethod01 extends AbstractPhilosopherMethod {

	@Override
	public void method(Philosopher p, AbstractChopstick[] cs) throws Exception {
		int left = p.getId();
		int right = (left + 1) % cs.length;

		p.take(cs[left]);
		p.take(cs[right]);

		p.eat();

		p.put(cs[left]);
		p.put(cs[right]);

		p.think();
	}

}

这个方法绝大多数情况下是能正常工作的，但是也是存在问题的，比如如果每个哲学家同时拿起左叉子，都在等待右叉子时就会造成死锁。
当然也不是不能打破这个死锁，可以设置等待超时时间。这样这个方案虽然不能避免死锁，但是能打破死锁。

死锁发生时的情况：

死锁发生

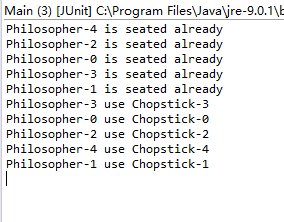
同时只允许一位哲学家就餐

同时只允许一位哲学家就餐，换句话说就是某一个哲学家取筷子的时候，把所有的筷子都霸占，使得其他哲学家都不能碰筷子。把所有的筷子作为一个整体是一个临界资源。

test.properties：

1
2
3

chopstick.class=com.chain.test.day04.Chopstick01
philosopher.class=com.chain.test.day04.Philosopher
philosopher.method.class=com.chain.test.day04.PhilosopherMethod02

package com.chain.test.day04;

/**
 * 同时只允许一位哲学家就餐
 * 
 * @author chain
 *
 */
public class PhilosopherMethod02 extends AbstractPhilosopherMethod {

	@Override
	public void method(Philosopher p, AbstractChopstick[] cs) throws Exception {
		int left = p.getId();
		int right = (left + 1) % cs.length;

		synchronized (cs) {
			p.take(cs[left]);
			p.take(cs[right]);
		}

		p.eat();

		p.put(cs[left]);
		p.put(cs[right]);

		p.think();
	}

}

这样做，会造成效率降低。从运行结果中可以看到运行速度降低，并且每次确实只有一个哲学家在抓筷子。

哲学家分成奇偶

死锁之所以会发生主要是在P操作，释放筷子的V操作不会发生阻塞。

test.properties：

1
2
3

chopstick.class=com.chain.test.day04.Chopstick01
philosopher.class=com.chain.test.day04.Philosopher
philosopher.method.class=com.chain.test.day04.PhilosopherMethod03

package com.chain.test.day04;

/**
 * 哲学家分成奇偶
 * 
 * @author chain
 *
 */
public class PhilosopherMethod03 extends AbstractPhilosopherMethod {

	@Override
	public void method(Philosopher p, AbstractChopstick[] cs) throws Exception {
		int id = p.getId();
		int left = id;
		int right = (left + 1) % cs.length;

		if ((id & 1) == 1) {
			p.take(cs[left]);
			p.take(cs[right]);
		} else {
			p.take(cs[right]);
			p.take(cs[left]);
		}

		p.eat();

		p.put(cs[left]);
		p.put(cs[right]);

		p.think();
	}

}

这样的解决可行，不过不算很通用。

当且仅当两个筷子都可以

要么不拿，要么就拿两把筷子。

哲学家此时就有三种状态：思考状态（不用筷子）、饥饿状态（等待左右筷子）、就餐状态（使用筷子）。

此时的操作就是对哲学家的状态的操作，哲学家的“状态”成为临界资源，而筷子就能合理分配，不需要再做互斥处理，可以简化设计。

当某个哲学家在饥饿状态时，他需要筷子吃饭，如果此时他的两边哲学家都不在就餐状态时，他就可以顺利的拿到左右手的筷子吃到饭，并进入就餐状态。
当某个哲学家在饥饿状态时，两边只要有一个在就餐，那么他就不可以拿到左右手的筷子，也就吃不到饭，一直保持饥饿状态（或者等待一会后放弃继续进入思考状态）。
当某个哲学家吃完饭后，放下筷子后通知两边的哲学家，接着进入思考状态。

test.properties：

1
2
3

chopstick.class=com.chain.test.day04.Chopstick01
philosopher.class=com.chain.test.day04.Philosopher
philosopher.method.class=com.chain.test.day04.PhilosopherMethod04

哲学家Status：

1
2
3

public enum Status {
	THINK, HUNGRY, EAT
}

使用Object的wait和notify实现对Status的PV操作。

package com.chain.test.day04;

/**
 * 当且仅当两个筷子都可以
 * 
 * 使用wait和notify
 * 
 * @author chain
 *
 */
public class PhilosopherMethod04 extends AbstractPhilosopherMethod {

	private volatile Status[] status;

	public PhilosopherMethod04() {
		status = new Status[Main.PHILOSOPHER_NUM];
		for (int i = 0; i < status.length; i++)
			status[i] = Status.HUNGRY;
	}

	@Override
	public void method(AbstractPhilosopher p, AbstractChopstick[] cs) throws Exception {
		takes(p, cs);

		p.eat();

		puts(p, cs);

		p.think();
	}

	/**
	 * 放下手中的筷子，并通知其他所有的哲学家
	 * 
	 * @param p
	 * @param cs
	 */
	private synchronized void puts(AbstractPhilosopher p, AbstractChopstick[] cs) {
		int id = p.getId();
		int right = (id + 1) % Main.PHILOSOPHER_NUM;
		p.put(cs[id]);
		p.put(cs[right]);
		status[p.getId()] = Status.THINK;
		this.notifyAll();
	}

	/**
	 * 尝试同时抓起两边的筷子
	 * 
	 * @param p
	 * @param cs
	 * @throws Exception
	 */
	private synchronized void takes(AbstractPhilosopher p, AbstractChopstick[] cs) throws Exception {
		int id = p.getId();
		status[id] = Status.HUNGRY;
		trial(p, cs);
		while (status[id] != Status.EAT) {
			this.wait();
			trial(p, cs);
		}
	}

	private synchronized void trial(AbstractPhilosopher p, AbstractChopstick[] cs) throws Exception {
		int id = p.getId();
		int n = Main.PHILOSOPHER_NUM;
		int left = (id - 1 + n) % n;
		int right = (id + 1) % n;
		if (status[id] == Status.HUNGRY && status[left] != Status.EAT && status[right] != Status.EAT) {
			p.take(cs[id]);
			p.take(cs[right]);
			status[id] = Status.EAT;
			this.notifyAll();
		}
	}

}

test.properties：

1
2
3

chopstick.class=com.chain.test.day04.Chopstick01
philosopher.class=com.chain.test.day04.Philosopher
philosopher.method.class=com.chain.test.day04.PhilosopherMethod05

使用ReentrantLock和Condition实现Status的PV操作。

package com.chain.test.day04;

import java.util.concurrent.locks.Condition;
import java.util.concurrent.locks.ReentrantLock;

/**
 * 当且仅当两个筷子都可以
 * 
 * 使用ReentrantLock和Condition
 * 
 * @author chain
 *
 */
public class PhilosopherMethod05 extends AbstractPhilosopherMethod {

	private ReentrantLock lock;
	private Condition[] cond;

	private volatile Status[] status;

	public PhilosopherMethod05() {
		status = new Status[Main.PHILOSOPHER_NUM];
		for (int i = 0; i < status.length; i++)
			status[i] = Status.HUNGRY;

		lock = new ReentrantLock();

		cond = new Condition[Main.PHILOSOPHER_NUM];
		for (int i = 0; i < cond.length; i++)
			cond[i] = lock.newCondition();
	}

	@Override
	public void method(AbstractPhilosopher p, AbstractChopstick[] cs) throws Exception {
		takes(p, cs);

		p.eat();

		puts(p, cs);

		p.think();
	}

	/**
	 * 放下手中的筷子，并通知两边的哲学家
	 * 
	 * @param p
	 * @param cs
	 */
	private void puts(AbstractPhilosopher p, AbstractChopstick[] cs) {
		lock.lock();
		try {
			int id = p.getId();
			int n = Main.PHILOSOPHER_NUM;
			int left = (id - 1 + n) % n;
			int right = (id + 1) % n;
			p.put(cs[id]);
			p.put(cs[right]);
			status[p.getId()] = Status.THINK;
			trial(left, cs);
			trial(right, cs);
		} finally {
			if (lock.isLocked())
				lock.unlock();
		}
	}

	/**
	 * 尝试同时抓起两边的筷子
	 * 
	 * @param p
	 * @param cs
	 * @throws Exception
	 */
	private void takes(AbstractPhilosopher p, AbstractChopstick[] cs) throws Exception {
		lock.lock();
		try {
			int id = p.getId();
			status[id] = Status.HUNGRY;
			trial(id, cs);
			while (status[id] != Status.EAT)
				cond[id].await();
			if (status[id] == Status.EAT) {
				int right = (id + 1) % Main.PHILOSOPHER_NUM;
				p.take(cs[id]);
				p.take(cs[right]);
			}
		} finally {
			if (lock.isLocked())
				lock.unlock();
		}
	}

	private void trial(int id, AbstractChopstick[] cs) {
		int n = Main.PHILOSOPHER_NUM;
		int left = (id - 1 + n) % n;
		int right = (id + 1) % n;
		if (status[id] == Status.HUNGRY && status[left] != Status.EAT && status[right] != Status.EAT) {
			status[id] = Status.EAT;
			cond[id].signal();
		}
	}

}

在别的博客看到还有另外一种做法，将筷子和哲学家进行颠倒，哲学家成为临界资源，而由筷子去选择哲学家。

思考总结

修改test.properties中的chopstick.class也是类似的效果，比如同时抓起左筷子并等待右筷子时会死锁。

正常的情况如下：

正常情况

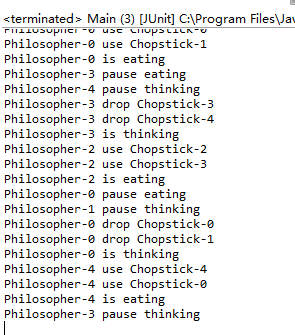
解决这个问题的一开始自然的想法就是，所有的哲学家先尝试去拿左边的筷子，如果拿到了就再去尝试拿右边的筷子，如果没有拿到左边的筷子，就一直处于饥饿状态，直到可以拿到左边的筷子。如果拿到了右边的筷子，哲学家就进入就餐状态，就餐状态执行一段时间后哲学家放下手中的两只筷子，并进入思考状态。放下筷子后两边的哲学家就可以得到他们需要的左手筷子或右手筷子。

这样的方法乍一看上去是没有问题的，但是如果所有的哲学家都同时成功的拿起了左边的筷子，然后去等待右边的筷子，而右边的筷子显然一直会被右边的哲学家抓在他的左手中。那么就会造成死锁。除非有哲学家主动放下左手中的筷子，这个死锁才可能解除。

解决这个问题的方法主要有三种。

第一种简单粗暴，就是只允许同时只有一个哲学家能去拿筷子，注意不是整个就餐，只要保证拿筷子的过程是独占的即可。这样的操作自然不会有死锁问题，缺陷就是原本最多可以有两个哲学家能同时并成功的拿到筷子，现在只能有一个。执行的效率会降低。

第二种比较有技巧性，就是将哲学家分成奇偶。奇数先尝试拿左再拿右，偶数先尝试拿右再拿左。这样仔细分析一下：如果奇数的哲学家先拿到了左手的筷子，然后去拿右手边的筷子，而与此同时偶数的哲学家（就在奇数的哲学家两旁），会先去尝试拿右边的筷子，左边的筷子只会在右边的筷子成功拿到后才会去尝试拿。对于奇数的哲学家来说，右手的筷子直接可以拿到，因为他旁边的哲学家（也是偶数哲学家）在尝试拿他的右手边的筷子，根本不会去管他左边的筷子。对于偶数的哲学家来说，他想先去拿右手边得筷子，但是发现右手边的筷子被他右边的哲学家已经握在了左手中，就会一直处于饥饿状态等待。当奇数的哲学家拿到筷子并饱餐一顿放下筷子后，偶数的哲学家也就能拿到一直渴望的右手边的筷子，拿到右手边的筷子后，由于奇数的哲学家刚刚吃完在思考并不会去碰筷子，偶数的哲学家也能顺利的拿到左手边的筷子开始就餐。这样循环下去，能正常执行。

第三种，对问题进行了升华。哲学家要么一次拿起面前的两双筷子开吃，要么就不拿。原本筷子是临界资源，这种方法将临界资源改为哲学家的“状态”（同时原本的筷子无需再进行独占设计）。哲学家的状态可以划分为三种：思考状态（无需筷子）、饥饿状态（需要筷子）、就餐状态（占有筷子）。具体分析一下：需要就餐，处在饥饿状态的哲学家会先看看他两边的哲学家的状态。如果两边的哲学家都沉浸在自己的思考中，即思考状态，并不需要筷子，那么这个哲学家可以拿起两边的筷子开始就餐，进入就餐状态。如果他两边只要有一个哲学家在就餐状态，那么也就意味着他面前的筷子是不足两只的，他就保持饥饿状态等待。就餐完毕的哲学家放下手中的筷子，在进入思考状态前“告知”一下旁边的两位哲学家，“我已经吃完，你们可以拿我刚放下的筷子了”，然后就立即进入思考状态。因为不会存在相邻两个哲学家都在就餐的情况，只会存在相邻两个哲学家都在思考或饥饿，所以获得通知的饥饿中的哲学家会再次尝试去判断他两边哲学家的状态，如果两边的哲学家都处于思考状态，那么这个哲学家可以拿起两边的筷子并进入就餐状态，如果仍然不行则继续等待。这种方法能保证最多两个哲学家同时就餐，最多三个哲学家同时在等待，不会都在等待状态，所以能正常执行。

经典问题搞懂，能做到举一反三。

源码