Java实现基于哈夫曼的压缩/解压缩算法

通信课信息论中介绍了哈夫曼编码，这里想着编程实现一下压缩和解压缩。

博主水平有限，有不正确的地方欢迎指正。

算法介绍

David Huffman和他的压缩算法 —— Huffman Code，是一种通过字符出现频率，结合 Priority Queue 和二叉树来进行的一种压缩算法，这种二叉树又叫Huffman二叉树（一种带权重的树）。他又被称为最优二叉树，是一类带权路径长度最短的树。

压缩可以分为无损压缩和有损压缩。

有损压缩，指的是压缩之后就无法完整还原原始信息，但是压缩率可以很高，主要应用于视频、话音等数据的压缩，因为损失了一点信息，人是很难察觉的，或者说，也没必要那么清晰照样可以看可以听。

无损压缩，则用于文件等等必须完整还原信息的场合，ZIP自然就是一种无损压缩，在通信原理中介绍数据压缩的时候，往往是从信息论的角度出发，引出香农所定义的熵的概念。

哈夫曼编码是一种无损编码，可以完全正确的压缩和还原数据，就是运算速度比较慢。

算法介绍可以参看这篇博客。

哈夫曼树具有如下特性：
1）对于同一组权值，所能得到的哈夫曼树不一定是唯一的。
2）哈夫曼树的左右子树可以互换，因为这并不影响树的带权路径长度。
3）带权值的节点都是叶子节点，不带权值的节点都是某棵子二叉树的根节点。
4）权值越大的节点越靠近哈夫曼树的根节点，权值越小的节点越远离哈夫曼树的根节点。
5）哈夫曼树中只有叶子节点和度为2的节点，没有度为1的节点。
6）一棵有n个叶子节点的哈夫曼树共有2n-1个节点。
7）每个字符编码不会成为另一个编码的前缀。

Huffman编码的过程大致如下：
1、统计一个文件以各个字符出现的次数
2、以各个字符出现的次数为权值建立哈夫曼树
3、根据哈夫曼树计算出每个字符的哈夫曼编码（可以用从树根到该字符所在到叶子节点的路径来表示）
4、将原文件的各个字符用编出的码字替换
5、将各个字符出现的次数信息和新生成的数据结合存储，则为压缩过程。

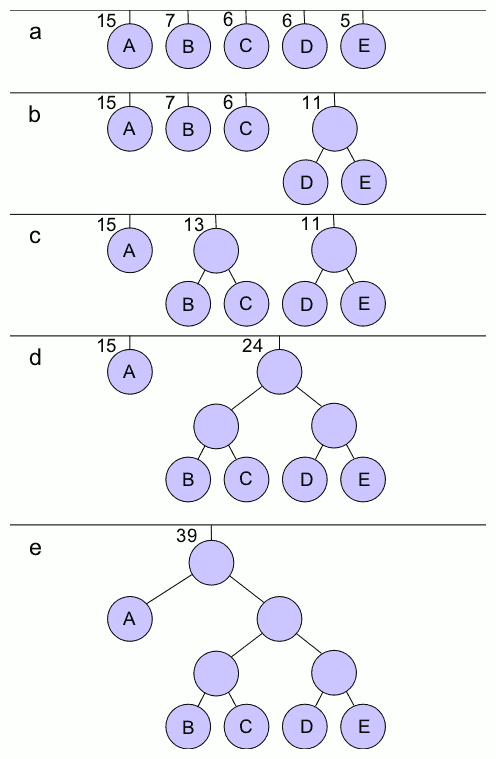
Huffmana解码的过程大致如下：
1、获得存储的压缩文件中的各个字符出现的次数信息
2、根据各个字符出现的次数信息重新构建哈夫曼树
3、对压缩数据依次进行检索，根据每次检索的位数据获得对应的哈夫曼码，进而获得对应的字符。
4、将翻译出的字符连接起来，则为解压缩过程。

构树的过程大致有两种(来自百度)：

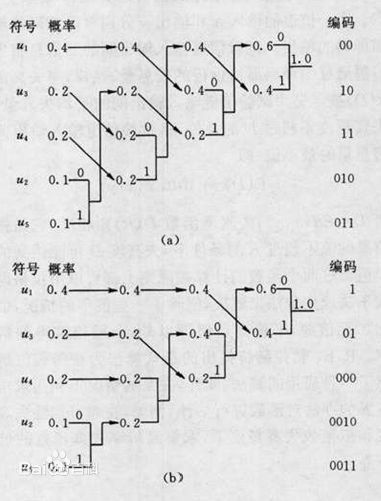
但是与这篇博客介绍的方法不同的是，本文实现的构树算法是采用(a)，而前者使用的是(b)。
方法(a)编出的码字更加均匀一点。

原本需要1B空间存储的数据，比如字符’a’，需要一个字节来存储，可能对应的哈夫曼编码只是11，即只需要两个bit来存储，进而起到压缩效果。

算法源码

源码可以从这里访问。

测试结果

这里就只贴出测试的结果。

java

orgin string: 11a11aa1aa1a111aaa
decode string: 11a11aa1aa1a111aaa
origin-data-length: 144
encode-data-length: 18
encode-times: 8.0
encode-percent: 0.13
decode-data-length: 144

orgin string: 11a11aa1aa1a111aaa
decode string: 11a11aa1aa1a111aaa
origin-data-length: 144
encode-data-length: 144
encode times: 1.0
encode percent: 1.0
decode-data-length: 144

orgin string: 我和他说你很好，他和我说你很好，他和你说我很好，我和你说他很好，你和我说他很好，你和他说我很好，你很好，我很好，她很好，他和我很好，你和我很好，你和他很好，他和我很好，他和你很好，我和你很好，我和他很好，你和他和他很好，我和他和他很好，他和你和你很好，他和我和他很好，很好很好很好很好很好很好很好很好很好很好很好，好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好
decode string: 我和他说你很好，他和我说你很好，他和你说我很好，我和你说他很好，你和我说他很好，你和他说我很好，你很好，我很好，她很好，他和我很好，你和我很好，你和他很好，他和我很好，他和你很好，我和你很好，我和他很好，你和他和他很好，我和他和他很好，他和你和你很好，他和我和他很好，很好很好很好很好很好很好很好很好很好很好很好，好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好好
origin-data-length: 4896
encode-data-length: 2241
encode-times: 2.18
encode-percent: 0.46
decode-data-length: 4896

orgin string: 我和他说你很好 ...
decode string: 我和他说你很好 ...
origin-data-length: 4896
encode-data-length: 3184
encode times: 1.54
encode percent: 0.65
decode-data-length: 4896

C:\Temps\huffman_test\test.txt
orgin string: 123abc123abc ...
decode string: 123abc123abc ...
origin-data-length: 10368
encode-data-length: 3456
encode-times: 3.0
encode-percent: 0.33
decode-data-length: 10368

orgin string: 123abc123abc ...
decode string: 123abc123abc ...
origin-data-length: 10368
encode-data-length: 3768
encode times: 2.75
encode percent: 0.36
decode-data-length: 10368

C:\Temps\huffman_test\数字.txt
origin-data-length: 5743272
encode-data-length: 2421825
encode-times: 2.37
encode-percent: 0.42
decode-data-length: 5743272

origin-data-length: 5743272
encode-data-length: 2422432
encode times: 2.37
encode percent: 0.42
decode-data-length: 5743272

C:\Temps\huffman_test\圣经.txt
origin-data-length: 35741304
encode-data-length: 20348325
encode-times: 1.76
encode-percent: 0.57
decode-data-length: 35741304

origin-data-length: 35741304
encode-data-length: 20352048
encode times: 1.76
encode percent: 0.57
decode-data-length: 35741304

C:\Temps\huffman_test\简爱.txt
origin-data-length: 8919976
encode-data-length: 5176611
encode-times: 1.72
encode-percent: 0.58
decode-data-length: 8919976

origin-data-length: 8919976
encode-data-length: 5180864
encode times: 1.72
encode percent: 0.58
decode-data-length: 8919976

C:\Temps\huffman_test\test.jpg
origin-data-length: 8535152
encode-data-length: 8285268
encode-times: 1.03
encode-percent: 0.97
decode-data-length: 8535152

origin-data-length: 8535152
encode-data-length: 8297584
encode times: 1.03
encode percent: 0.97
decode-data-length: 8535152

C:\Temps\huffman_test\test.bmp
origin-data-length: 3026224
encode-data-length: 467555
encode-times: 6.47
encode-percent: 0.15
decode-data-length: 3026224

origin-data-length: 3026224
encode-data-length: 469120
encode times: 6.45
encode percent: 0.16
decode-data-length: 3026224

C:\Temps\huffman_test\test.mp4
origin-data-length: 4956832
encode-data-length: 4955436
encode-times: 1.0
encode-percent: 1.0
decode-data-length: 4956832

origin-data-length: 4956832
encode-data-length: 4967752
encode times: 1.0
encode percent: 1.0
decode-data-length: 4956832

C:\Temps\huffman_test\test.exe
origin-data-length: 27959936
encode-data-length: 20832169
encode-times: 1.34
encode-percent: 0.75
decode-data-length: 27959936

origin-data-length: 27959936
encode-data-length: 20844488
encode times: 1.34
encode percent: 0.75
decode-data-length: 27959936

C:\Temps\huffman_test\test.zip
origin-data-length: 110320
encode-data-length: 110023
encode-times: 1.0
encode-percent: 1.0
decode-data-length: 110320

origin-data-length: 110320
encode-data-length: 122336
encode times: 0.9
encode percent: 1.11
decode-data-length: 110320

C:\Temps\huffman_test\test.pdf
origin-data-length: 13177832
encode-data-length: 13163269
encode-times: 1.0
encode-percent: 1.0
decode-data-length: 13177832

origin-data-length: 13177832
encode-data-length: 13175584
encode times: 1.0
encode percent: 1.0
decode-data-length: 13177832

worst test
origin-data-length: 2048
encode-data-length: 2048
encode-times: 1.0
encode-percent: 1.0
decode-data-length: 2048

汇总如下（不严谨）：

文件类型	压缩比
纯数字(txt)	0.42
英文文学(txt)	0.58
图片(jpg)	0.97
图片(bmp)	0.16
视频(mp4)	1.0
程序(exe)	0.75
压缩文件(zip)	1.0
pdf	1.0

最糟糕的情况就是：文本中总共有256种字符，每种字符出现的频率（次数、概率）相同；或者在二进制文件中，每个字节的二进制都存在，即有256种情况，每种情况出现的概率相同。这样编出来的哈夫曼树也是一颗满二叉树，树的高度为9。

测试中的部分详细信息如下：

第一个测试：
orgin string: 11a11aa1aa1a111aaa
decode string: 11a11aa1aa1a111aaa
origin-data-length: 144
encode-data-length: 18
encode-times: 8.0
encode-percent: 0.13
decode-data-length: 144

detail: 
huffman-tree-height: 2
huffman-statistics-table: 
0, key: 49, times: 9
1, key: 97, times: 9
origin-data-length: 144
encode-data-length: 18
encode-times: 8.0
encode-percent: 0.13

最糟糕的测试：
worst test
origin-data-length: 2048
encode-data-length: 2048
encode-times: 1.0
encode-percent: 1.0
decode-data-length: 2048

detail: 
huffman-tree-height: 9
huffman-statistics-table: 
0, key: 0, times: 1
1, key: 1, times: 1
2, key: 2, times: 1
3, key: 3, times: 1
...
n, key: n, times: 1
...
253, key: 253, times: 1
254, key: 254, times: 1
255, key: 255, times: 1
origin-data-length: 2048
encode-data-length: 2048
encode-times: 1.0
encode-percent: 1.0

补充说明

计算一下哈夫曼编码的压缩性能。

假设在计算中忽略哈夫曼树的本身额外的存储（换句话说，只有原文件不仅体积大，而且包含的字符数量多时才可以忽略哈夫曼本身的存储消耗）。

用len表示原数据串长度，path(i)表示每i个字符的编码长度。
那么根据原理可以知道，原数据串通过哈夫曼压缩后的长度为：

hlen = sum(path(i)) ; 1 <= i <= len

这个式子虽然正确但是不直观，所以假设一种平均情况进行估算：

假如一个串长度为n，一共包含m个不同的字符，那么所构建成的哈夫曼树的总结点数为 2*m-1。

如果n很大，那么可以忽略树本身的保存所需要占用的空间。

如果假设此串中每个字符出现的次数都是相同的，那么也可以假设，它们所生成的哈夫曼树是完全二叉树。
即每个叶子(字符)的深度为log(m)+1，则路径长度为log(m)。

log(m) 即为该串字符的平均路径长度，那么压缩后的串长为log(m)/8。

由上可以得出平均压缩比的公式为：

n log(2 m - 1)/8/n = log(2 * m - 1)/8;

可见压缩比的大小主要与m有关，即不同的字符越少越好。

ASCII码的范围为0～255，共有256种不同字符，代入上式得：

log(2*256-1) ＝ 6.23 …

向上取整为7(路径个数哪有小数)。
进一步有：

7/8 = 0.875 = %87.5

所以哈夫曼编码的平均压缩比为 %87.5。

参考文章

伯乐在线
 csdn
wikipedia

LEECHAIN | 博客

Java实现基于哈夫曼的压缩算法