N皇后问题

发表于 | 分类于

N皇后问题（常见解法 Java实现）

N皇后问题也是算法题中的经典题目，也有很多种不同的解法。这里就实现并总结一下常见的解法。

背景简介

N皇后问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：

在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

image

主要是回溯思想的体现。

下面将介绍常见的N皇后四种做法，当然还有很多其他的做法。

递归求解

N皇后问题，在递归解法下，第一种自然的做法是采用二维数组来表示棋盘。

二维数组表示棋盘还是比较直观好理解的。

贴上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
package com.chain.algorithm.test.day02;

import java.time.Duration;
import java.time.Instant;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

/**
 * 八皇后问题的递归解法-二维数组
 * 
 * @author Chain
 *
 */
public class NQueen01 {

	// 总共有多少种解法
	private int count;
	// 二维数组表示棋盘
	private boolean[][] chess;
	// 皇后的数量
	private int N;
	// 记录具体的结果
	private List<int[]> result;

	private NQueen01() {
		this(8);
	}

	private NQueen01(int n) {
		this.N = n;
	}

	private NQueen01(int n, boolean save) {
		this(n);
		if (save)
			result = new ArrayList<>();
	}

	public static Map<String, Object> calc(int n) {
		return calc(n, false);
	}

	public static Map<String, Object> calc(int n, boolean save) {
		NQueen01 nq = new NQueen01(n, save);
		nq.chess = new boolean[n][n];

		Instant start = Instant.now();
		nq.put(0);
		Instant end = Instant.now();

		Map<String, Object> res = new HashMap<>();
		res.put("count", nq.count);
		res.put("time", Duration.between(start, end).toMillis());
		res.put("result", nq.result);
		return res;
	}

	private void put(int row) {
		if (row == N) {
			add();
			return;
		}

		for (int i = 0; i < N; i++)
			if (check(row, i)) {
				chess[row][i] = true;
				put(row + 1);
				reset(row);
			}
	}

	private void reset(int row) {
		Arrays.fill(chess[row], false);
	}

	private boolean check(int row, int pos) {
		// 倒过来，从下而上
		for (int i = row - 1; i > -1; i--) {
			// 垂直方向
			if (chess[i][pos])
				return false;
			// 反斜线方向（左斜）
			if (pos - row + i > -1 && chess[i][pos - row + i])
				return false;
			// 正斜线方向（右斜）
			if (pos + row - i < N && chess[i][pos + row - i])
				return false;
		}
		return true;
	}

	private void add() {
		count++;

		if (result == null)
			return;

		int[] r = new int[N];
		for (int i = 0; i < N; i++)
			for (int j = 0; j < N; j++)
				if (chess[i][j])
					r[i] = j + 1;

		result.add(r);
	}

}

递归方法-二维数组方法的测试结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
queen: 4
count: 2
time: 0
result: 
1: 2 4 1 3 
2: 3 1 4 2 

queen: 8
count: 92
time: 2
result: null

queen: 16
count: 14772512
time: 734411
result: null

分析代码可知，二维数组的情况下，在比较时的操作次数是非常惊人的，下面尝试使用一维数组来进行改进。

第二种做法，将二维数组改成一维数组。既降低了时间复杂度，也压缩了空间复杂度。

一维数组下标表示棋盘的行数，值表示该行的皇后放置的位置。

贴上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
package com.chain.algorithm.test.day02;

import java.time.Duration;
import java.time.Instant;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

/**
 * 八皇后问题的递归解法-一维数组
 * 
 * @author Chain
 *
 */
public class NQueen02 {

	// 总共有多少种解法
	private int count;
	// 一维数组表示棋盘（存储皇后放置的位置）
	private int[] chess;
	// 皇后的数量
	private int N;
	// 记录具体的结果
	private List<int[]> result;

	private NQueen02() {
		this(8);
	}

	private NQueen02(int n) {
		this.N = n;
	}

	private NQueen02(int n, boolean save) {
		this(n);
		if (save)
			result = new ArrayList<>();
	}

	public static Map<String, Object> calc(int n) {
		return calc(n, false);
	}

	public static Map<String, Object> calc(int n, boolean save) {
		NQueen02 nq = new NQueen02(n, save);
		nq.chess = new int[n];

		Instant start = Instant.now();
		nq.put(0);
		Instant end = Instant.now();

		Map<String, Object> res = new HashMap<>();
		res.put("count", nq.count);
		res.put("time", Duration.between(start, end).toMillis());
		res.put("result", nq.result);
		return res;
	}

	private void put(int row) {
		if (row == N) {
			add();
			return;
		}

		for (int i = 0; i < N; i++)
			if (check(row, i)) {
				chess[row] = i;
				put(row + 1);
			}
	}

	private boolean check(int row, int pos) {
		/// 倒过来
		for (int i = row - 1; i > -1; i--) {
			// 垂直
			if (chess[i] == pos)
				return false;
			// 斜线
			if (Math.abs(row - i) == Math.abs(pos - chess[i]))
				return false;
		}
		return true;
	}

	private void add() {
		count++;

		if (result == null)
			return;

		int[] r = new int[N];
		for (int i = 0; i < N; i++)
			r[i] = chess[i] + 1;

		result.add(r);
	}

}

递归方法-一维数组方法的测试结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
queen: 4
count: 2
time: 0
result: 
1: 2 4 1 3 
2: 3 1 4 2 

queen: 8
count: 92
time: 0
result: null

queen: 16
count: 14772512
time: 388009
result: null

由此可见，在递归方法下使用一维数组的话效率提升近一倍。

当然还有一种改进，就是用手动栈来代替系统栈，不过就单从效率上比较的话，和使用系统递归的做法相比不明显，不如直接使用循环。

循环求解

这里使用一维数组来记录值，将递归改造成循环。效率和递归相比，没有多少变化。

贴上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
package com.chain.algorithm.test.day02;

import java.time.Duration;
import java.time.Instant;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

/**
 * 八皇后问题的循环解法-一维数组
 * 
 * @author Chain
 *
 */
public class NQueen03 {

	// 总共有多少种解法
	private int count;
	// 一维数组表示棋盘（存储皇后放置的位置）
	private int[] chess;
	// 皇后的数量
	private int N;
	// 记录具体的结果
	private List<int[]> result;

	private NQueen03() {
		this(8);
	}

	private NQueen03(int n) {
		this.N = n;
	}

	private NQueen03(int n, boolean save) {
		this(n);
		if (save)
			result = new ArrayList<>();
	}

	public static Map<String, Object> calc(int n) {
		return calc(n, false);
	}

	public static Map<String, Object> calc(int n, boolean save) {
		NQueen03 nq = new NQueen03(n, save);
		nq.chess = new int[n];

		Instant start = Instant.now();
		nq.put();
		Instant end = Instant.now();

		Map<String, Object> res = new HashMap<>();
		res.put("count", nq.count);
		res.put("time", Duration.between(start, end).toMillis());
		res.put("result", nq.result);
		return res;
	}

	private void put() {
		int row = 0;
		Arrays.fill(chess, -1);
		while (row >= 0) {
			chess[row]++;
			while (chess[row] < N && !check(row, chess[row]))
				chess[row]++;
			if (chess[row] < N) {
				if (row == N - 1)
					add();
				else
					row++;
			} else {
				chess[row] = -1;
				row--;
			}
		}
	}

	private boolean check(int row, int pos) {
		/// 倒过来
		for (int i = row - 1; i > -1; i--) {
			// 垂直
			if (chess[i] == pos)
				return false;
			// 斜线
			if (Math.abs(row - i) == Math.abs(pos - chess[i]))
				return false;
		}
		return true;
	}

	private void add() {
		count++;

		if (result == null)
			return;

		int[] r = new int[N];
		for (int i = 0; i < N; i++)
			r[i] = chess[i] + 1;

		result.add(r);
	}

}

循环方法-一维数组方法的测试结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
queen: 4
count: 2
time: 0
result: 
1: 2 4 1 3 
2: 3 1 4 2 

queen: 8
count: 92
time: 0
result: null

queen: 16
count: 14772512
time: 428106
result: null

位运算法

由于数据在计算机中是以二进制的形式存储的，因此位运算指令的执行速度是很快的。如果判断冲突时,能够使用位运算代替算术运算,可以取得较高的运行效率。

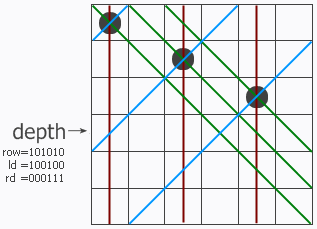
image

位运算采用递归做法，循环做法并不能带来明显的效率提升。

贴上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
package com.chain.algorithm.test.day02;

import java.time.Duration;
import java.time.Instant;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

/**
 * 
 * 八皇后问题的递归解法-位运算
 * 
 * @author Chain
 *
 */
public class NQueen04 {

	// 总共有多少种解法
	private int count;
	// 整数表示棋盘（存储棋盘的大小，在这里最多是32）
	private int chess;
	// 皇后的数量
	private int N;
	// 记录具体的结果
	private List<int[]> result;

	private NQueen04() {
		this(8);
	}

	private NQueen04(int n) {
		this.N = n;
	}

	private NQueen04(int n, boolean save) {
		this(n);
		if (save)
			result = new ArrayList<>();
	}

	public static Map<String, Object> calc(int n) {
		return calc(n, false);
	}

	public static Map<String, Object> calc(int n, boolean save) {
		NQueen04 nq = new NQueen04(n, save);
		nq.chess = (1 << n) - 1;

		Instant start = Instant.now();
		nq.put();
		Instant end = Instant.now();

		Map<String, Object> res = new HashMap<>();
		res.put("count", nq.count);
		res.put("time", Duration.between(start, end).toMillis());
		res.put("result", nq.result);
		return res;
	}

	private void put() {
		int[] r = new int[N];
		fun(0, 0, 0, 0, r);
	}

	// 位运算求解，col表示列，ld表示反斜线（左斜），rd表示正斜线（右斜）
	// 整个放置皇后的过程是每次都是按列从右往左尝试放置，每次执行时对应棋盘的行数为该次递归调用的次数
	// t为递归调用的次数，也是棋盘对应的操作的行数
	private void fun(int col, int ld, int rd, int t, int[] r) {
		if (col == chess) {
			add(r);
			return;
		}

		// col列，ld，rd进行逻辑或运算，求得当前行不能放置皇后的位置，均为1
		// 再取反，就可以求得当前行可以放置皇后的位置，均为1
		// 再和chess进行逻辑与，是为了去除超出棋盘的位置（ld，rd）
		int empty = chess & ~(col | ld | rd);
		// 用来记录从右往左看第一个可以放置皇后的位置
		int p;
		// 判断还有没有地方可以放置
		while (empty != 0) {
			// 获得从右往左看第一个可以放置皇后的位置
			// -empty 等价于 ~empty + 1
			p = empty & -empty;

			// 在p位置放置皇后，该位置0
			empty -= p;

			// 存储
			save(r, t, p);

			// col | p 表示col列已经被放置了皇后，下一次就不能再放在col列了
			// (ld + p) << 1 表示col列放置皇后后，下一次左斜不能再放置皇后的位置
			// (rd | p) >> 1 表示col列放置皇后后，下一次右斜不能再放置皇后的位置
			// 等价做法（位运算更快）：fun(col + p, (ld + p) << 1, (rd + p) >> 1, t + 1, r);
			fun(col | p, (ld | p) << 1, (rd | p) >> 1, t + 1, r);
		}
	}

	private void save(int[] r, int t, int p) {
		if (result == null)
			return;

		int i = 1;
		// p不会为0
		while (p != 1) {
			p >>>= 1;
			i++;
		}
		r[t] = i;
	}

	private void add(int[] r) {
		count++;

		if (result == null)
			return;

		result.add(r.clone());
	}
}

递归方法-位运算方法的测试结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
queen: 4
count: 2
time: 0
result: 
1: 2 4 1 3 
2: 3 1 4 2 

queen: 8
count: 92
time: 0
result: null

queen: 16
count: 14772512
time: 13153
result: null

由此可见，使用位运算的速度提升是非常明显的，这也是目前比较快的做法。

在求解的结果中，可以发现有些是对称的，因此还可以进行进一步的剪枝，这里就不做研究了。

测试代码

最后再补充贴上测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
package com.chain.algorithm.test.day02;

import java.util.List;
import java.util.Map;

import org.junit.Test;

public class NQueueTest {

	@Test
	public void test1() {
		print(4, NQueen01.calc(4, true));
		print(8, NQueen01.calc(8, false));
		print(16, NQueen01.calc(16, false));
	}

	@Test
	public void test2() {
		print(4, NQueen02.calc(4, true));
		print(8, NQueen02.calc(8, false));
		print(16, NQueen02.calc(16, false));
	}

	@Test
	public void test3() {
		print(4, NQueen03.calc(4, true));
		print(8, NQueen03.calc(8, false));
		print(16, NQueen03.calc(16, false));
	}

	@Test
	public void test4() {
		print(4, NQueen04.calc(4, true));
		print(8, NQueen04.calc(8, false));
		print(16, NQueen04.calc(16, false));
	}

	@SuppressWarnings("unchecked")
	private void print(int qn, Map<String, Object> res) {
		System.out.println("queen: " + qn);
		System.out.println("count: " + res.get("count"));
		System.out.println("time: " + res.get("time"));
		List<int[]> result = (List<int[]>) res.get("result");
		System.out.print("result: ");
		if (result == null) {
			System.out.println("null");
			return;
		}
		System.out.println();
		int len = result.size();
		for (int i = 0; i < len; i++) {
			int[] a = result.get(i);
			System.out.print((i + 1) + ": ");
			for (int j = 0; j < a.length; j++)
				System.out.print(a[j] + " ");
			System.out.println();
		}
	}

}

参考博客

cnblogs