群硕校招-同色三角形

发表于 | 分类于

群硕校招-同色三角形

这是一道编程题，一开始还想到了图的遍历。后来仔细阅读后发现，这条题目其实还是挺简单的。

考试题目

平面上有6个点，每两个点之间都以红线或黑线连接，任意三点均不共线。现在，已知下列点之间的连线是红色的，剩下的连线都是黑色的。要求计算这些点组成的三角形中有多少是同色的?

已知的红色连线(6,5) (1,2) (1,3) (2,3) (2,5) (3,6)。

我的解决

一开始以为线相交的点也要算进去，甚至还想到用图来解决。再次阅读后，发现使用暴力法就能解决问题。

先画个图，方便分析。

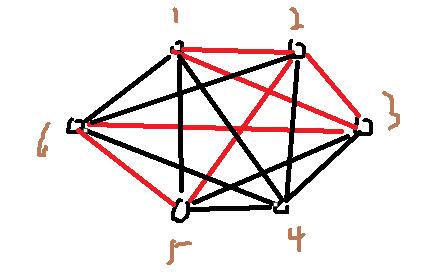
image

6个点总共可以构成的三角形数量为C[6,3]=20。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
package com.chain.blog.test.day11;

import java.util.Scanner;

//同色三角形
public class QunShuoTest2 {

	public static void main(String[] args) {
		test1();
	}

	private static void test1() {
		try (Scanner in = new Scanner(System.in)) {
			// 点个数
			int n = in.nextInt();
			// 红色连线个数
			int m = in.nextInt();
			// 红色连线存储，邻接矩阵
			int[][] t = new int[n][n];
			for (int i = 0; i < m; i++) {
				int d1 = in.nextInt() - 1;
				int d2 = in.nextInt() - 1;
				t[d1][d2] = 1;
				t[d2][d1] = 1;
			}
			long sum = 0;
			long tri = 0;
			// 从第一个点开始依次暴力
			for (int i = 0; i < n - 2; i++) {
				for (int j = i + 1; j < n - 1; j++) {
					for (int k = j + 1; k < n; k++) {
						int s1 = t[i][j];
						int s2 = t[j][k];
						int s3 = t[i][k];
						if (s1 == s2 && s2 == s3) {
							sum += 1;
							System.out.println("发现同色三角形：" + (i + 1) + " " + (j + 1) + " " + (k + 1));
						}
						tri += 1;
					}
				}
			}
			System.out.println("总共有三角形个数：" + tri);
			System.out.println("同色三角形的个数：" + sum);
		}
	}
}

测试结果

测试是按照题意输入的数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
6 6
6 5
1 2
1 3
2 3
2 5
3 6
发现同色三角形：1 2 3
发现同色三角形：1 4 5
发现同色三角形：1 4 6
发现同色三角形：2 4 6
发现同色三角形：3 4 5
总共有三角形个数：20
同色三角形的个数：5

其他答案

可能还有其他的更好的解答吧。