常见的数组排序算法（补充）

发表于 | 分类于

常见的数组排序算法（Java版 补充）

之前写过一篇排序的算法，原文链接。

现在再来补充其他的一些算法，或者原来算法的改进方法，并结合一些其他的博文，做一些知识点总结。

推荐一个常见算法的动态演示网站：https://visualgo.net/

本文：
源码在这里。
测试在这里。

文中插图来自网络。

排序算法

一些排序算法的补充或改进。

笔试面试最常涉及到的12种排序算法：

冒泡排序、鸡尾酒排序；插入排序、二分插入排序，希尔排序；选择排序；快速排序；堆排序；归并排序；桶排序；计数排序；基数排序。

鸡尾酒排序

这种排序算法又被称为鸡尾酒排序，或者叫定向冒泡排序。

这种改进算法与传统的冒泡排序的不同之处在于：从低到高然后又从高到低，而冒泡排序则仅是从低到高的去比较。

鸡尾酒排序可以得到比冒泡排序稍微好一点的效能，但是在乱数序列的状态下，鸡尾酒排序与冒泡排序的效率都很差劲。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
* 定向冒泡排序，或鸡尾酒排序：从低到高然后又从高到低
* 
* @param a
*            要排序的数组
*/
public static void cockTailSort(int[] a) {
    checkArray(a);
    int n = a.length;
    boolean flag = false;// false代表没有排好序
    int left = 0;
    int right = n - 1;
    while (left < right && !flag) {
        // 先从左到右，升序
        for (int i = left; i < right && !flag; i++) {
            if (a[i] > a[i + 1]) {
                flag = false;
                swap(a, i, i + 1);
            }
        }
        if (flag)
            break;
        right--;
        // 在从右到左，降序
        for (int i = right; i > left && !flag; i--) {
            if (a[i - 1] > a[i]) {
                flag = false;
                swap(a, i - 1, i);
            }
        }
        if (flag)
            break;
        left++;
    }
}

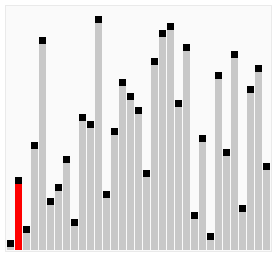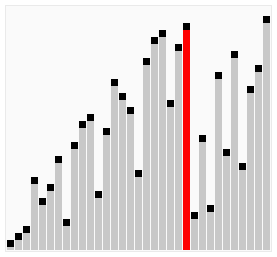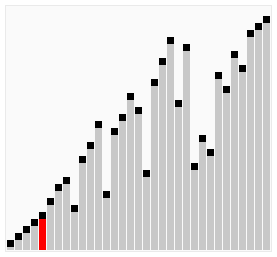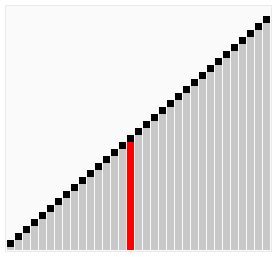
image

二分插入排序

插入排序中，要插入的元素再找到自己的插入位置时，是依次（顺序）查找，这样的查找比较缓慢。所以可以融入二分查找，以提高在查找插入位置时的效率。

当n较大时，二分插入排序的比较次数比直接插入排序的最差情况好得多，但比直接插入排序的最好情况要差，所当以元素初始序列已经接近升序时，直接插入排序比二分插入排序比较次数少。

但是，二分插入排序元素移动次数与直接插入排序相同，依赖于元素初始序列，减少的是查找时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
* 类二分查找的插入排序，适合元素数量较多的情况。
* 
* @param a
*            要排序的数组
*/
public static void binarySearchInsertSort(int[] a) {
    checkArray(a);
    int n = a.length;
    for (int i = 1; i < n; i++) {
        int t = a[i];
        int left = 0;
        int right = i - 1;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            if (a[mid] > t)
                right = mid - 1;
            else
                left = mid + 1;
        }
        for (int j = i - 1; j >= left; j--) {
            a[j + 1] = a[j];
        }
        a[left] = t;
    }
}

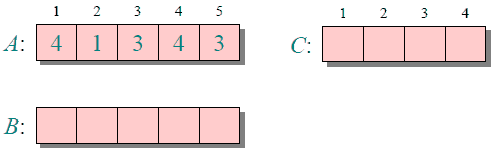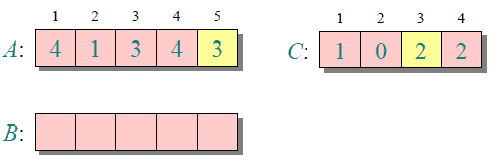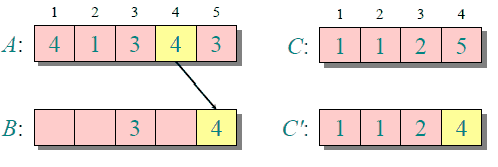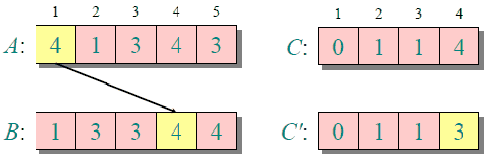
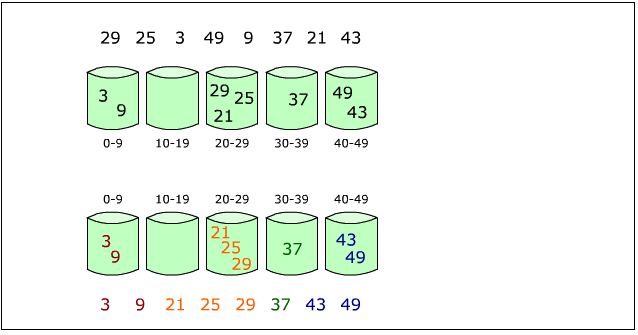
计数排序

非比较型排序算法，在排序的时候就知道元素的正确位置，那么只需扫描一遍即可放入正确位置。如此以来，只需知道有多大范围就可以了。这就是计数排序的思想。

性能：时间复杂度O(n+k)，线性时间，并且稳定。
优点：不需比较，利用地址偏移，对范围固定在[0,k]的整数排序的最佳选择。是排序字符串最快的排序算法。
缺点：用来计数的数组的长度取决于带排序数组中数据的范围（等于待排序数组的最大值和最小值的差加1），这使得计数排序对于数据范围很大的数组，需要大量时间和空间，即牺牲空间换取时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
    * 计数排序：适用于数值范围较小的数组，比如字符串排序，0-9排序等。
    * 
    * 非比较排序
    * 
    * @param a
    *            要排序的数组
    */
public static void countSort(int[] a) {
    checkArray(a);
    int n = a.length;
    int[] r = new int[n];
    int max = a[0];
    int min = max;
    for (int i : a) {
        if (i > max)
            max = i;
        if (i < min)
            min = i;
    }
    // 用于统计
    int len = max - min + 1;
    int[] f = new int[len];
    // 统计出现的次数
    for (int i = 0; i < n; i++)
        f[a[i] - min]++;
    // 计算相对位移
    for (int i = 1; i < len; i++)
        f[i] += f[i - 1];
    // 倒序输出数组（稳定）
    for (int i = n - 1; i > -1; i--)
        r[--f[a[i] - min]] = a[i];
    // 再拷贝回去
    for (int i = 0; i < n; i++)
        a[i] = r[i];
}

image

归并排序

归并排序是创建在归并操作上的一种有效的排序算法，效率为O(nlogn)。1945年由冯·诺伊曼首次提出。

归并排序的实现分为递归实现与非递归(迭代)实现。

递归实现的归并排序：是算法设计中分治策略的典型应用，我们将一个大问题分割成小问题分别解决，然后用所有小问题的答案来解决整个大问题。
非递归(迭代)实现的归并排序：首先进行是两两归并，然后四四归并，然后是八八归并，一直下去直到归并了整个数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/**
* 归并排序：自顶而下，递归做法
* 
* @param a
*            要排序的数组
*/
public static void mergeSort(int[] a) {
    checkArray(a);
    int n = a.length;
    int low = 0;
    int high = n - 1;
    mergeSortPartSort(a, low, high);
}

private static void mergeSortPartMerge(int[] a, int low, int mid, int high) {
    // 两个指针
    int p = low;
    int q = mid + 1;
    int len = high - low + 1;
    // 临时数组，用于排序的备份
    int[] t = new int[len];
    for (int i = low; i <= high; i++)
        t[i - low] = a[i];
    for (int i = low; i <= high; i++) {
        // 左半边已无剩余
        if (p > mid) {
            a[i] = t[q++ - low];
        }
        // 右半边已无剩余
        else if (q > high) {
            a[i] = t[p++ - low];
        }
        // 右半边当前元素小于左半边当前元素，取右半边的元素
        else if (t[q - low] < t[p - low]) {
            a[i] = t[q++ - low];
        }
        // 右半边当前元素大于或等于左半边当前元素，取左半边的元素
        else {
            a[i] = t[p++ - low];
        }
    }
}

// 自顶而下，递归做法
private static void mergeSortPartSort(int[] a, int low, int high) {
    // 分到每组一个元素为止
    if (low >= high)
        return;

    int mid = (high - low) / 2 + low;
    // 左右两边分治，分别进行排序
    mergeSortPartSort(a, low, mid);
    mergeSortPartSort(a, mid + 1, high);
    // 左右两边归并
    mergeSortPartMerge(a, low, mid, high);
}

/**
* 归并排序：自底而上，循环做法
* 
* @param a
*            要排序的数组
*/
public static void buttomUpMergeSort(int[] a) {
    checkArray(a);
    int n = a.length;
    int high = n - 1;
    // 进行logN次两两归并
    // p代表size
    int delta = 0;
    for (int p = 1; p <= high; p = delta) {
        delta = p << 1;
        // 每个size下对每一个划分的小组进行归并
        for (int low = 0; low <= high - p; low += delta) {
            mergeSortPartMerge(a, low, low + p - 1, Math.min(low + delta - 1, high));
        }
    }
}

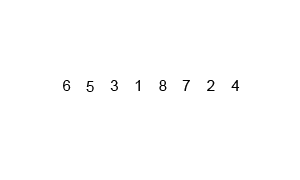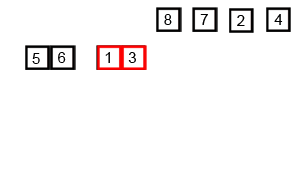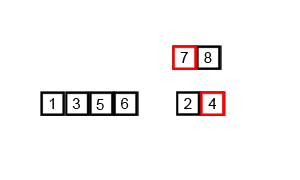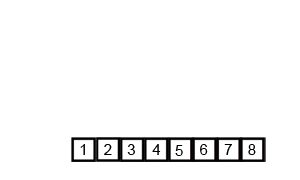
image

image

image

对归并排序进行一些改进可以提高合并排序的效率。

  1. 当划分到较小的子序列时，通常可以使用插入排序替代合并排序。
  2. 如果已经排好序了就不用合并了。
  3. 并行化。

归并排序和快速排序一样都是时间复杂度为nlgn的算法，但是和快速排序相比，合并排序是一种稳定性排序，也就是说排序关键字相等的两个元素在整个序列排序的前后，相对位置不会发生变化，这一特性使得合并排序是稳定性排序中效率最高的一个。在Java中对引用对象进行排序，Perl、C++、Python的稳定性排序的内部实现中，都是使用的合并排序。

具体可以参考这篇博客。

基数排序

非比较型排序算法，原理是将整数按位切割成不同数字，然后按每个位数分别比较。

将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零，然后从最低位开始，依次进行一次排序，这样从最低位排序一直到最高位排序完成后，数列就变成有序的。

基数排序会使用到计数排序作为每一位数位时的排序方式。

因为是0-9排序，所以中间过程使用计数排序相对较快，当然也可以使用其他排序方式。

基数排序的时间复杂度是O(n*dn)，其中n是待排序元素个数，dn是数字位数。这个时间复杂度不一定优于O(nlogn)，dn的大小取决于数字位的选择（比如比特位数），和待排序数据所属数据类型的全集的大小；

数字位数dn决定了需要进行多少次处理，而n是每次处理的操作数目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
    * 基数排序：非比较排序算法，这里是最低位优先基数排序LSD(Least significant digit)
    * 
    * @param a
    *            要排序的数组
    */
public static void radixSort(int[] a) {
    checkArray(a);
    radixSort(a, 10);
}

private static void radixSort(int[] a, int radix) {
    int max = a[0];
    int min = max;
    for (int i : a) {
        if (i > max)
            max = i;
        if (i < min)
            min = i;
    }
    // 最大和最小的差
    int delta = max - min;
    // 指数
    int exponent = 1;
    // 从低位开始往高位依次进行按位计数排序
    while (delta / exponent >= 1) {
        countSortByDigit(a, radix, exponent, delta, min);
        exponent *= radix;
    }
}

private static void countSortByDigit(int[] a, int radix, int exponent, int delta, int min) {
    int n = a.length;
    // 用于统计
    int len = delta + 1;
    int[] f = new int[len];
    // 统计出现的次数（频率）
    int findex = 0;
    for (int i = 0; i < n; i++) {
        // 取数组元素的第exponent位。
        // 比如exponent等于1，则取最后一位（个位）；exponent等于10，则取十位。
        // 如果超过位数，则计算下来也正好是0，起到补0的效果。
        findex = ((a[i] - min) / exponent) % radix;
        f[findex]++;
    }
    // 计算相对位移
    for (int i = 1; i < len; i++)
        f[i] += f[i - 1];
    // 反序输出到中间数组（这样确保稳定）
    int[] r = new int[n];
    for (int i = n - 1; i > -1; i--) {
        findex = ((a[i] - min) / exponent) % radix;
        r[--f[findex]] = a[i];
    }
    // 再拷贝回去
    for (int i = 0; i < n; i++)
        a[i] = r[i];
}

如果考虑和比较排序进行对照，基数排序的形式复杂度虽然不一定更小，但由于不进行比较，因此其基本操作的代价较小，而且如果适当的选择基数，dn一般不大于logn，所以基数排序一般要快过基于比较的排序，比如快速排序。

由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序除了可以进行整数排序，也可以进行其他排序。

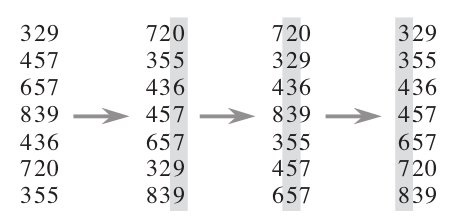
image

桶排序

桶排序也叫箱排序，为非比较型排序算法。

工作的原理是将数组元素映射到有限数量个桶里，利用计数排序可以定位桶的边界，每个桶再各自进行桶内排序（可以使用其它排序算法或以递归方式继续使用桶排序）。

就像分拣邮件那样。主要在于桶的大小和桶的数量的选择，这里的桶的大小和桶的数量的选择仅做参考。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
    * 桶排序：先使用计数排序进行分桶操作，然后对每个非空桶进行排序。
    * 
    * 非比较排序，又叫箱排序。
    * 
    * @param a
    *            要排序的数组
    */
public static void bucketSort(int[] a) {
    checkArray(a);
    int n = a.length;
    int max = a[0];
    int min = max;
    for (int i : a) {
        if (i > max)
            max = i;
        if (i < min)
            min = i;
    }
    // 桶的容量
    int size = 1;
    int delta = max - min;
    int t = delta;
    while (t > 0) {
        size *= DECIMAL;
        t /= 10;
    }
    // 桶的数量
    int bs = n % size == 0 ? n / size : n / size + 1;
    // 记录桶的边缘
    int[] b = new int[bs];
    // 计数排序进行分桶
    countSortForBucket(a, b, size, min);
    // 每个桶进行单独排序
    for (int i = 0; i < bs; i++) {
        int start = b[i];
        int end = i == bs - 1 ? n - 1 : b[i + 1] - 1;
        // 这里使用选择排序，其他排序方法也是可以的
        selectSortForBucket(a, start, end);
    }
}

private static void countSortForBucket(int[] a, int[] bucket, int size, int min) {
    int n = a.length;
    int bn = bucket.length;
    int[] r = new int[n];
    // 统计出现的次数
    int findex = 0;
    for (int i = 0; i < n; i++) {
        findex = (a[i] - min) / size;
        bucket[findex]++;
    }
    // 计算相对位移
    for (int i = 1; i < bn; i++)
        bucket[i] += bucket[i - 1];
    // 倒序输出数组（稳定）
    for (int i = n - 1; i > -1; i--) {
        findex = (a[i] - min) / size;
        // 桶的边缘被更新：bucket[i]为第i号桶中第一个元素所在r中的位置
        r[--bucket[findex]] = a[i];
    }
    // 再拷贝回去
    for (int i = 0; i < n; i++)
        a[i] = r[i];
}

private static void selectSortForBucket(int[] a, int start, int end) {
    // 都是闭合区间
    for (int i = start; i < end; i++) {
        int min = i;
        for (int j = i + 1; j <= end; j++) {
            if (a[j] < a[min])
                min = j;
        }
        if (min != i) {
            swap(a, min, i);
        }
    }
}

桶排序不是比较排序，不受到O(nlogn)下限的影响，它是鸽巢排序的一种归纳结果，当所要排序的数组值分散均匀的时候，桶排序拥有线性的时间复杂度。

什么时候是最好情况呢？
输入数组在一个范围内均匀分布。

什么时候是最坏情况呢？
数组的所有元素都进入同一个桶。

image

堆排序

堆排序是指利用堆这种数据结构所设计的一种选择排序算法。堆是一种近似完全二叉树的结构（通常堆是通过一维数组来实现的）。

以最大堆（也叫大根堆、大顶堆）为例，其中父结点的值总是大于它的孩子节点，或完全二叉树中所有非叶子结点的值均不大于（或不小于）其左、右孩子结点的值。

堆排序其实也是一种选择排序，是一种树形选择排序。

其基本思想为(大顶堆)：
1） 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
2） 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
3） 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成，得到升序序列。

以上思想可归纳为两个操作：
1）根据初始数组去构造初始堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大）。
2）每次交换第一个和最后一个元素，输出最后一个元素（最大值），然后把剩下元素重新调整为大根堆。
当输出完最后一个元素后，这个数组已经是按照从小到大的顺序排列了。

若想得到升序，则建立大顶堆；若想得到降序，则建立小顶堆。

对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

堆排序的具体原理和过程这两篇博客1和博客2讲的很好。

如下图，这是一个初始堆，接下来的代码可以参考这个图。

image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/**
    * 堆排序：利用数组来实现堆，利用堆的性质来排序。
    * 
    * 因为这个堆是使用数组实现的，所以元素节点不需要复杂操作的左孩子和右孩子，只是有数学上的关系而已。
    * 
    * 堆的含义是：完全二叉树中所有非叶子结点的值均不大于（或不小于）其左、右孩子结点的值。
    * 
    * @param a
    */
public static void heapSort(int[] a) {
    checkArray(a);
    int n = a.length;
    // 构造初始大顶堆
    heapSortBuild(a);
    // 无序区的元素个数大于1，则代表未完成排序
    // n==1时即排序完成，最后一个元素无需调整
    while (n > 1) {
        // 每次将第一个元素（堆顶元素）和最后一个元素（叶子节点）交换
        // 交换不仅会破环原来的堆结构，也会改变相对位置，所以堆排序是非稳定的
        swap(a, 0, --n);
        // 从新的堆顶元素开始向下重新进行堆调整，使其成为一个新堆，时间复杂度O(logn)
        heapify(a, 0, n);
    }
}

// 构建大顶堆其实也是堆调整的过程
private static void heapSortBuild(int[] a) {
    int n = a.length;
    // 从最后一个非叶子结点开始向上进行调整
    for (int i = n / 2 - 1; i > -1; i--) {
        heapify(a, i, n);
    }
}

// 堆调整，对大小为0-size的堆中第index个元素进行调整，使其满足大顶堆
private static void heapify(int[] a, int index, int size) {
    // 该节点，节点的左孩子，节点的右孩子哪个最大
    int max = index;
    // 左孩子节点是该节点的2*index+1
    int left = 2 * index + 1;
    if (left < size && a[left] > a[max])
        max = left;
    // 右孩子节点是该节点的2*index+2
    int right = 2 * index + 2;
    if (right < size && a[right] > a[max])
        max = right;
    if (max != index) {
        // 将最大的节点调整为父节点
        swap(a, max, index);
        // 递归调用，继续将交换到max节点的被破坏部分进行调整
        heapify(a, max, size);
    }
}

image

image

image

动画在排序过程之前简单的表现了创建堆的过程以及堆的逻辑结构。

堆排序是不稳定的排序算法，不稳定发生在堆顶元素与A[i]交换的时刻。

堆排序方法对记录数较少的文件并不值得提倡，但对n较大的文件还是很有效的。因为其运行时间主要耗费在建初始堆和调整建新堆时进行的反复“筛选”上。

堆排序在最坏的情况下，其时间复杂度也为O(nlogn)。相对于快速排序来说，这是堆排序的最大优点。此外，堆排序仅需一个记录大小的供交换用的辅助存储空间。

堆排序的应用在于优先级队列，比如绝大多数手机分配给来电的优先级都会比其他应用高。

排序小结

排序分内排序和外排序。

内排序:指在排序期间数据对象全部存放在内存的排序。
外排序:指在排序期间全部对象个数太多,不能同时存放在内存,必须根据排序过程的要求,不断在内、外存之间移动的排序。

内排序的方法有许多种,按所用策略不同,可归纳为五类:插入排序、选择排序、交换排序、归并排序、分配排序和计数排序。

插入排序主要包括直接插入排序，折半插入排序和希尔排序两种;
选择排序主要包括直接选择排序和堆排序;
交换排序主要包括冒泡排序和快速排序;
归并排序主要包括二路归并(常用的归并排序)和自然归并。
分配排序主要包括箱排序和基数排序。
计数排序就一种。

基于比较排序的算法，时间复杂度下界是O(nlogn)。
非比较类型的排序算法如计数排序，桶排序，基数排序，是可以突破O(nlogn)的下界的。
换句话说非比较类型的排序可能比基于排序的算法更好。
但是非基于比较的排序算法使用限制比较多。
比如：
计数排序进对较小整数进行排序，且要求排序的数据规模不能过大；
基数排序可以对长整数进行排序，但是不适用于浮点数；
桶排序可以对浮点数进行排序。

排序的稳定

稳定排序:假设在待排序的文件中,存在两个或两个以上的记录具有相同的关键字,在用某种排序法排序后,若这些相同关键字的元素的相对次序仍然不变,则这种排序方法是稳定的。

其中冒泡,插入,基数,归并属于稳定排序;
选择,快速,希尔,堆属于不稳定排序。

排序算法稳定性的简单形式化定义为：

如果Ai = Aj，排序前Ai在Aj之前，排序后Ai还在Aj之前，则称这种排序算法是稳定的。通俗地讲就是保证排序前后两个相等的数的相对顺序不变。

对于不稳定的排序算法，只要举出一个实例，即可说明它的不稳定性；

而对于稳定的排序算法，必须对算法进行分析从而得到稳定的特性。

需要注意的是，排序算法是否为稳定的是由具体算法决定的，不稳定的算法在某种条件下可以变为稳定的算法，而稳定的算法在某种条件下也可以变为不稳定的算法。
例如，对于冒泡排序，原本是稳定的排序算法，如果将记录交换的条件改成A[i] >= A[i + 1]，则两个相等的记录就会交换位置，从而变成不稳定的排序算法。
其次，说一下排序算法稳定性的好处。排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。基数排序就是这样，先按低位排序，逐次按高位排序，低位排序后元素的顺序在高位也相同时是不会改变的。

每种排序算法都各有优缺点。因此，在实用时需根据不同情况适当选用，甚至可以将多种方法结合起来使用。

算法的选择

影响排序的因素有很多，平均时间复杂度低的算法并不一定就是最优的。相反，有时平均时间复杂度高的算法可能更适合某些特殊情况。同时，选择算法时还得考虑它的可读性，以利于软件的维护。一般而言，需要考虑的因素有以下四点：

1．待排序的记录数目n的大小；
2．记录本身数据量的大小，也就是记录中除关键字外的其他信息量的大小；
3．关键字的结构及其分布情况；
4．对排序稳定性的要求。

设待排序元素的个数为n.

1）当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
堆排序：如果内存空间允许且要求稳定性的，
归并排序：它有一定数量的数据移动，所以我们可能过与插入排序组合，先获得一定长度的序列，然后再合并，在效率上将有所提高。

2）当n较大，内存空间允许，且要求稳定性 =》归并排序

3）当n较小，可采用直接插入或直接选择排序。

直接插入排序：当元素分布有序，直接插入排序将大大减少比较次数和移动记录的次数。
直接选择排序 ：元素分布有序，如果不要求稳定性，选择直接选择排序

5）一般不使用或不直接使用传统的冒泡排序。

6）基数排序：
它是一种稳定的排序算法，但有一定的局限性：
a、关键字可分解。
b、记录的关键字位数较少，如果密集更好
c、如果是数字时，最好是无符号的，否则将增加相应的映射复杂度，可先将其正负分开排序。

算法基本思想

常见的内部排序算法（摘自软考书）。

直接插入排序的基本思想：
每步将个待排序的记录按其排序码值的大小，插到前面己经排好的文件中的适当位置，直到全部插入完为止。

希尔排序的基本思想：
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分成d1个组，所有距离为d的倍数的记录放在间一个组中。先在各维内进行直接插入排序，然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量dt=1(dt<dt-1<O<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。该方法实质上是一种分组插入方法。

直接选择择序的基本思想:
首先在所有记录中选出排序码最小的记录，把它与第1个记录交换，然后在其余的记录内选出排序码最小的记录，与第2个记录交换…依此类推，直到所有记录排完为止，

堆排序的基本思想：
堆挂序是一种树形选择排序，是对直接选择排序的有效改进。它通过建立初始堆和不断地重建堆，逐个地将排序关键字按顺序输出，从而达到排序的目的。

冒泡排序的基本思想：
将被排序的记录数组R[1..n]重直排列，每个记录R[i]看作是重量为ki的气泡。根据轻气泡不能在重气泡之下的原则，从F往上扫描数组R，凡扫描到违反本原则的轻气泡，就使其向上“飘浮”。如此反复进行，直到最后任何两个气泡都是轻者在上，重者在下为止。

快速排序的基本思想:
采用了一种分治的策略，将原问题分解为若于个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题的解组合为原问题的解。

归并排序的基本思想:
将两个或两个以上的有序子表合并成个新的有序表。初始时，把含有n个结点的待排序序列看作由n个长度都为1的有序子表所组成，将它们依次两两归并得到长度为2的若千有序子表，再对它们两两合并，直到得到长度为n的有序表为止，排序结束。

基数排序的基本思想:
从低位到高位依次对待排序的关键码进行分配和收集，经过d趟分配和收集，就可以得到一个有序序列。

参考文章

1、csdn
2、cnblogs
3、cnblogs
4、segmentfault
5、cnblogs