斐波那契数列

发表于 | 分类于

斐波那契数列

放完国庆假期，自己也该投入学习中了。先温故学习一下斐波那契数列，又称黄金分割数列，它是算法题经典中的经典，斐波那契数列在数学和生活以及自然界中都非常有用，具体的编程求解方法也有很多。这里整理一下，做个记录。

起源定义

参考知乎。

斐波那契数列最早被提出是印度数学家Gopala，他在研究箱子包装物件长度恰好为1和2时的方法数时首先描述了这个数列。

也就是这个问题：

有n个台阶，你每次只能跨一阶或两阶，上楼有几种方法？

而最早研究这个数列的当然就是斐波那契（Leonardo Fibonacci）了，他当时是为了描述如下情况的兔子生长数目：

第一个月初有一对刚诞生的兔子
第二个月之后（第三个月初）它们可以生育
每月每对可生育的兔子会诞生下一对新兔子
兔子永不死去

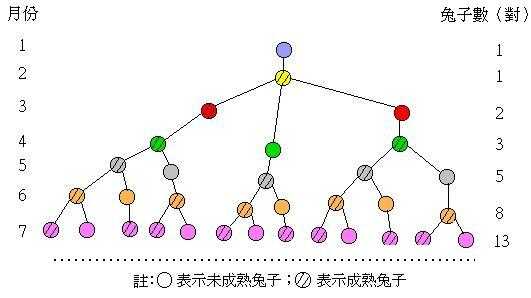
image

这个数列出自他赫赫有名的大作《计算之书》，后来就被广泛的应用于各种场合了。

这个数列是这么定义的：

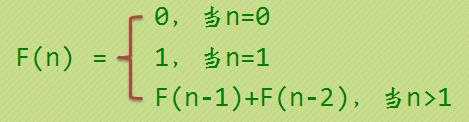
image

（注意，并非满足第三条的都是斐波那契数列，卢卡斯数列（A000032 - OEIS）也满足这一特点，但初始项定义不同）

求解方法

目前整理了斐波那契数列的4种解法。

斐波那契数列：

Fib(0) = 0
Fib(1) = 1
Fib(n) = Fib(n-1) + Fib(n-2)
F() = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …

在生活中，斐波那契数列有如下的自然现象：

image

诸如此类的还有向日葵、蜂巢、蜻蜓翅膀、海螺、人类耳朵轮廓等等。

递归做法

递归还是挺好理解的，斐波那契数列也是递归原理讲解的经典题目。

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
    * 递归做法，递归图是一个树形结构
    * 
    * 时间复杂度：O(2^n)
    * 
    * @param n
    * @return
    */
public int recursion(int n) {
    if (n < 2)
        return n;
    return recursion(n - 1) + recursion(n - 2);
}

由于每一次调用recursion方法都会再调用recursion两次，就像树节点下的两个子节点。斐波那契数列树因此而来。

比如求解f(5)，有以下的树结构：

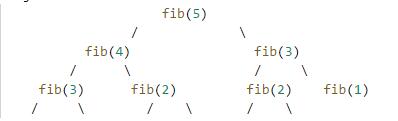
image

递归调用的时间复杂度是很恐怖的，O(n)=2^n。如果计算超过100，计算速度就很慢了，而且可能会造成栈溢出异常。

循环做法

循环做法可以借助一个数组，来存储中间的计算过程，便于查询和计算。

比如算n=50后，再计算n=6可以直接在数组中取即可，无需再计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
    * 循环做法(借助数组，可以用于打印前n个元素)
    * 
    * 时间复杂度：O(n)
    * 
    * @param n
    * @return
    */
public int circle(int n) {
    if (n < 2)
        return n;

    int[] f = new int[n + 1];
    f[1] = 1;

    for (int i = 2; i <= n; i++)
        f[i] = f[i - 1] + f[i - 2];

    return f[n];
}

当然，也可以直接计算，减少存储空间的浪费。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
    * 循环做法(无数组，直接计算，无需记忆)
    * 
    * 时间复杂度：O(n)
    * 
    * @param n
    * @return
    */
public int circleWithoutArray(int n) {
    if (n < 2)
        return n;

    int f0 = 0;
    int f1 = 1;
    int f2 = f0 + f1;

    for (int i = 2; i <= n; i++) {
        f2 = f0 + f1;
        f0 = f1;
        f1 = f2;
    }

    return f2;
}

循环做法在时间复杂度上肯定是优于递归做法的。

矩阵做法

参考博客。

矩阵做法需要一定的线性代数的知识，主要是矩阵的相乘，矩阵的基本性质，单位矩阵。

矩阵的基本性质回顾：

乘法结合律：(AB)C=A(BC)．
乘法左分配律：(A+B)C=AC+BC
乘法右分配律：C(A+B)=CA+CB
对数乘的结合性：k(AB=(kA)B=A(kB)
转置：(AB)T=BTAT
矩阵乘法一般不满足交换律。

首先是矩阵的相乘：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
    * 两个二阶矩阵相乘
    * 
    * 注意：只有第一个矩阵的列的个数等于第二个矩阵的行的个数，这样的两个矩阵才能相乘。
    * 
    * @param m1
    * @param m2
    * @return
    */
private int[][] multiply(int[][] m1, int[][] m2) {
    // m1c == m2r
    int m1r = m1.length;
    int m2r = m2.length;
    int m1c = m1[0].length;
    int m2c = m2[0].length;

    // m*p x p*n = m*n
    int[][] m3 = new int[m1r][m2c];
    for (int i = 0; i < m1r; i++) {
        for (int j = 0; j < m2c; j++) {
            int sum = 0;
            for (int k = 0; k < m1c; k++) {
                sum += m1[i][k] * m2[k][j];
            }
            m3[i][j] = sum;
        }
    }

    return m3;
}

然后是一个矩阵的n次幂，矩阵的幂就是矩阵的连乘：

比如：

1
16=2*2*2*2

类比于

1
A^9=A*((A^2)^2)^2)

代码的话可以这样编写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
    * 某一个二阶矩阵的n次快速幂
    * 
    * 例：<br>
    * 1）A^9 = A*((A^2)^2)^2) <br>
    * 2）A^15 = ((A^2)^2)^2)*((A^2)^2)*(A^2)*A
    * 
    * 二分分治思想，将其由线性的转为对数的
    * 
    * @param m
    * @param n
    * @return
    */
private int[][] pow(int[][] m, int n) {
    int e = m.length;
    int[][] r = new int[e][e];
    // 构建单位矩阵
    for (int i = 0; i < e; i++)
        r[i][i] = 1;
    while (n > 1) {
        int i = 1;
        int[][] s = m;
        while (true) {
            int t = i << 1;
            if (t > n)
                break;
            s = multiply(s, s);
            i = t;
        }
        n -= i;
        r = multiply(r, s);
    }
    if (n == 1)
        r = multiply(r, m);
    return r;
}

接下来就是斐波那契数列递推公式的推导过程了：

数列的递推公式为：f(1)=1，f(2)=2，f(n)=f(n-1)+f(n-2) (n>=3)

用矩阵表示为：

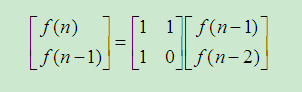
image

进一步，可以得出直接推导公式：

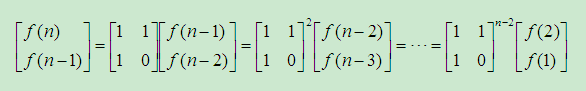
image

由于矩阵乘法满足结合律，在程序中可以事先给定矩阵的64，32，16，8，4，2，1次方，加快程序的执行时间。
给定的矩阵次幂，与二进制有关是因为，如下的公式存在解，满足Xi={0或1}：

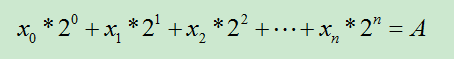
image

为了保证解满足 Xi={0或1}，对上述公式的求解从右向左，即求解顺序为Xn,Xn-1,Xn-2,….,X1,X0。

公式做个概括就是如下：

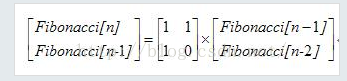
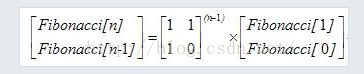
image

image

有了公式，再结合上面的矩阵运算的方法，可以很轻松的写出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
    * 矩阵做法，根据矩阵运算公式即可，计算无误差。
    * 
    * 时间复杂度：O(logn)
    * 
    * @param n
    * @return
    */
public int matrix(int n) {
    if (n < 2)
        return n;

    int[][] m = { { 1, 1 }, { 1, 0 } };
    int[][] f = { { 1 }, { 0 } };
    int[][] r = multiply(pow(m, n - 1), f);
    return r[0][0];
}

使用矩阵的n次快速幂，可以使得计算由线性而升高一个纬度，转为对数计算，计算时间大大减少。

算法的时间复杂度为O(n)=logn。

公式做法

公式的推导过程可以参考百度百科，目前有三种证明方法，分别是初等代数下的利用待定系数法构造等比数列的两种方法和利用线性代数中矩阵特征方程求解。

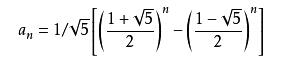
image

值得注意的是公式本身是正确的，而在于计算机在计算根号和除法时可能会有误差。

这里粘上特征方程证明法：

image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
    * 公式做法，通项公式，推导可以参考百度百科；<br>
    * 注意：公式本身没有误差，但是计算会有一定的误差。
    * 
    * 时间复杂度：O(1)
    * 
    * @param n
    * @return
    */
public int formula(int n) {
    if (n < 2)
        return n;

    double sqrt5 = Math.sqrt(5);
    double phi = (1 + sqrt5) / 2.0;
    Double fn = (Math.pow(phi, n) - Math.pow(1 - phi, n)) / sqrt5;
    return fn.intValue();
}

测试结果

先贴上完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
/**
 * 求解斐波那契数列，仅为算法演示，不考虑溢出和其他特殊情况
 * 
 * @author Chain
 *
 */
class Fibonacci {

	/**
	 * 递归做法，递归图是一个树形结构
	 * 
	 * 时间复杂度：O(2^n)
	 * 
	 * @param n
	 * @return
	 */
	public int recursion(int n) {
		if (n < 2)
			return n;
		return recursion(n - 1) + recursion(n - 2);
	}

	/**
	 * 循环做法(借助数组，可以用于打印前n个元素)
	 * 
	 * 时间复杂度：O(n)
	 * 
	 * @param n
	 * @return
	 */
	public int circle(int n) {
		if (n < 2)
			return n;

		int[] f = new int[n + 1];
		f[1] = 1;

		for (int i = 2; i <= n; i++)
			f[i] = f[i - 1] + f[i - 2];

		return f[n];
	}

	/**
	 * 循环做法(无数组，直接计算，无需记忆)
	 * 
	 * 时间复杂度：O(n)
	 * 
	 * @param n
	 * @return
	 */
	public int circleWithoutArray(int n) {
		if (n < 2)
			return n;

		int f0 = 0;
		int f1 = 1;
		int f2 = f0 + f1;

		for (int i = 2; i <= n; i++) {
			f2 = f0 + f1;
			f0 = f1;
			f1 = f2;
		}

		return f2;
	}

	/**
	 * 公式做法，通项公式，推导可以参考百度百科；<br>
	 * 注意：公式本身没有误差，但是计算会有一定的误差。
	 * 
	 * 时间复杂度：O(1)
	 * 
	 * @param n
	 * @return
	 */
	public int formula(int n) {
		if (n < 2)
			return n;

		double sqrt5 = Math.sqrt(5);
		double phi = (1 + sqrt5) / 2.0;
		Double fn = (Math.pow(phi, n) - Math.pow(1 - phi, n)) / sqrt5;
		return fn.intValue();
	}

	/**
	 * 矩阵做法，根据矩阵运算公式即可，计算无误差。
	 * 
	 * 时间复杂度：O(logn)
	 * 
	 * @param n
	 * @return
	 */
	public int matrix(int n) {
		if (n < 2)
			return n;

		int[][] m = { { 1, 1 }, { 1, 0 } };
		int[][] f = { { 1 }, { 0 } };
		int[][] r = multiply(pow(m, n - 1), f);
		return r[0][0];
	}

	/**
	 * 两个二阶矩阵相乘
	 * 
	 * 注意：只有第一个矩阵的列的个数等于第二个矩阵的行的个数，这样的两个矩阵才能相乘。
	 * 
	 * @param m1
	 * @param m2
	 * @return
	 */
	private int[][] multiply(int[][] m1, int[][] m2) {
		// m1c == m2r
		int m1r = m1.length;
		int m2r = m2.length;
		int m1c = m1[0].length;
		int m2c = m2[0].length;

		// m*p x p*n = m*n
		int[][] m3 = new int[m1r][m2c];
		for (int i = 0; i < m1r; i++) {
			for (int j = 0; j < m2c; j++) {
				int sum = 0;
				for (int k = 0; k < m1c; k++) {
					sum += m1[i][k] * m2[k][j];
				}
				m3[i][j] = sum;
			}
		}

		return m3;
	}

	/**
	 * 某一个二阶矩阵的n次快速幂
	 * 
	 * 例：<br>
	 * 1）A^9 = A*((A^2)^2)^2) <br>
	 * 2）A^15 = ((A^2)^2)^2)*((A^2)^2)*(A^2)*A
	 * 
	 * 二分分治思想，将其由线性的转为对数的
	 * 
	 * @param m
	 * @param n
	 * @return
	 */
	private int[][] pow(int[][] m, int n) {
		int e = m.length;
		int[][] r = new int[e][e];
		// 构建单位矩阵
		for (int i = 0; i < e; i++)
			r[i][i] = 1;
		while (n > 1) {
			int i = 1;
			int[][] s = m;
			while (true) {
				int t = i << 1;
				if (t > n)
					break;
				s = multiply(s, s);
				i = t;
			}
			n -= i;
			r = multiply(r, s);
		}
		if (n == 1)
			r = multiply(r, m);
		return r;
	}

	// 打印二维数组
	private void print(int[][] m) {
		int r = m.length;
		int c = m[0].length;
		for (int i = 0; i < r; i++) {
			for (int j = 0; j < c; j++) {
				System.out.print(m[i][j] + " ");
			}
			System.out.println();
		}
	}

	public static void main(String[] args) {
		Fibonacci f = new Fibonacci();
		int[][] m1 = { { 3, 4, 2 }, { 5, 4, 3 } };
		int[][] m2 = { { 5, 2, 1, 8 }, { 4, 3, 1, 9 }, { 5, 3, 4, 6 } };
		int[][] m3 = f.multiply(m1, m2);
		int[][] m4 = { { 1, 1 }, { 1, 0 } };
		int[][] m5 = f.pow(m4, 3);
		f.print(m3);
		f.print(m5);
	}

}

再贴上测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public class FibonacciTest {

	private static Fibonacci fibonacci = new Fibonacci();

	public static void main(String[] args) {
		Random rand = new Random();

		int n = rand.nextInt(100);

		n = 10;

		System.out.println("n is " + n);

		long start = System.currentTimeMillis();

		test1(n);
		long step1 = System.currentTimeMillis();

		test2(n);
		long step2 = System.currentTimeMillis();

		test3(n);
		long step3 = System.currentTimeMillis();

		test4(n);
		long step4 = System.currentTimeMillis();

		test5(n);
		long step5 = System.currentTimeMillis();

		System.out.println("test1 is " + (step1 - start));
		System.out.println("test2 is " + (step2 - step1));
		System.out.println("test3 is " + (step3 - step2));
		System.out.println("test4 is " + (step4 - step3));
		System.out.println("test5 is " + (step5 - step4));
	}

	private static void test1(int n) {
		int r = fibonacci.recursion(n);
		System.out.println("recursion：" + r);
	}

	private static void test2(int n) {
		int r = fibonacci.circle(n);
		System.out.println("circle：" + r);
	}

	private static void test3(int n) {
		int r = fibonacci.circleWithoutArray(n);
		System.out.println("circleWithoutArray：" + r);
	}

	private static void test4(int n) {
		int r = fibonacci.matrix(n);
		System.out.println("matrix：" + r);
	}

	private static void test5(int n) {
		int r = fibonacci.formula(n);
		System.out.println("formula：" + r);
	}

}

测试结果：

分别测试在n比较小情况下，和n比较大的情况下的测试结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
当n=10时：
n is 10
recursion：55
circle：55
circleWithoutArray：55
matrix：55
formula：55
test1 is 0
test2 is 0
test3 is 0
test4 is 0
test5 is 0

当n较大时，递归几乎无法计算。

文末总结

斐波那契数列经典但也时编程的基本功题目。同时，它也能体现很多编程的技巧和算法的思想，比如理解递归，包含动态规划和分治的思想。

具体的经典变形比如：跳台阶，矩形覆盖（参见《剑指Offer》）。