算法的时间和空间复杂度

发表于 | 分类于

算法的时间和空间复杂度

算法分析是很重要的过程，一个算法的好坏由很多因素可以判断。算法也是应用的精髓，比如导航中的算法等等。

算法分析

为什么要进行算法分析

预测算法所需的资源：

计算时间（CPU 消耗）
内存空间（RAM 消耗）
通信时间（带宽消耗）

预测算法的运行时间：

在给定输入规模时，所执行的基本操作数量。或者称为算法复杂度（Algorithm Complexity）。

如何衡量算法复杂度

内存（Memory）
时间（Time）
指令的数量（Number of Steps）
特定操作的数量
磁盘访问数量
网络包数量

渐进复杂度（Asymptotic Complexity）

算法的运行时间与什么相关

取决于输入的数据。（例如：如果数据已经是排好序的，时间消耗可能会减少。）
取决于输入数据的规模。（例如：6 和 6 * 109）
取决于运行时间的上限。（因为运行时间的上限是对使用者的承诺。）

算法分析的种类

最坏情况（Worst Case）：任意输入规模的最大运行时间。（Usually）
平均情况（Average Case）：任意输入规模的期待运行时间。（Sometimes）
最佳情况（Best Case）：通常最佳情况不会出现。（Bogus）

例如，在一个长度为 n 的列表中顺序搜索指定的值，则
最坏情况：n 次比较
平均情况：n/2 次比较
最佳情况：1 次比较

而实际中，我们一般仅考量算法在最坏情况下的运行情况，也就是对于规模为 n 的任何输入，算法的最长运行时间。
这样做的理由是：
一个算法的最坏情况运行时间是在任何输入下运行时间的一个上界（Upper Bound）。
对于某些算法，最坏情况出现的较为频繁。
大体上看，平均情况通常与最坏情况一样差。

算法分析要保持大局观（Big Idea），其基本思路：
忽略掉那些依赖于机器的常量。
关注运行时间的增长趋势。

比如：T(n) = 73n3 + 29n3 + 8888 的趋势就相当于 T(n) = Θ(n3)。

渐近记号（Asymptotic Notation）通常有 O、 Θ 和 Ω 记号法。

Θ 记号渐进地给出了一个函数的上界和下界，当只有渐近上界时使用 O 记号，当只有渐近下界时使用 Ω 记号。

尽管技术上 Θ 记号较为准确，但通常仍然使用 O 记号表示。

使用 O 记号法（Big O Notation）表示最坏运行情况的上界。

例如：
线性复杂度 O(n) 表示每个元素都要被处理一次。
平方复杂度 O(n2) 表示每个元素都要被处理 n 次。

例如：
T(n) = O(n3) 等同于 T(n) ∈ O(n3)
T(n) = Θ(n3) 等同于 T(n) ∈ Θ(n3).
相当于:
T(n) 的渐近增长不快于 n3。
T(n) 的渐近增长与 n3 一样快。

注1：logab = y 其实就是 ay = b。所以，log24 = 2，因为 22 = 4。同样 log28 = 3，因为 23 = 8。我们说，log2n 的增长速度要慢于 n，因为当 n = 8 时，log2n = 3。
注2：通常将以 10 为底的对数叫做常用对数。为了简便，N 的常用对数 log10 N 简写做 lg N，例如 log10 5 记做 lg 5。
注3：通常将以无理数 e 为底的对数叫做自然对数。为了方便，N 的自然对数 loge N 简写做 ln N，例如 loge 3 记做 ln 3。
注4：在算法导论中，采用记号 lg n = log2 n ，也就是以 2 为底的对数。改变一个对数的底只是把对数的值改变了一个常数倍，所以当不在意这些常数因子时，我们将经常采用 “lg n”记号，就像使用 O 记号一样。计算机工作者常常认为对数的底取 2 最自然，因为很多算法和数据结构都涉及到对问题进行二分。

计算代码块的渐进运行时间的方法有如下步骤：
确定决定算法运行时间的组成步骤。
找到执行该步骤的代码，标记为 1。
查看标记为 1 的代码的下一行代码。如果下一行代码是一个循环，则将标记 1 修改为 1 倍于循环的次数 1 x n。
如果包含多个嵌套的循环，则将继续计算倍数，例如 1 x n x m。
找到标记到的最大的值，就是运行时间的最大值，即算法复杂度描述的上界。

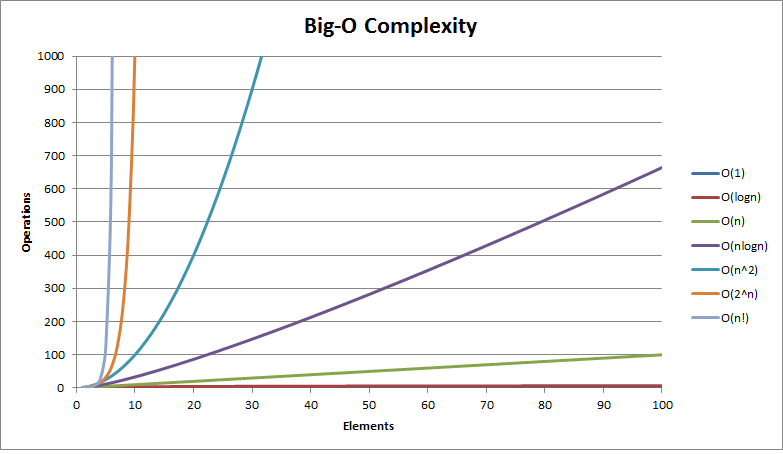
下面是一些常见的算法复杂度的直观函数图：

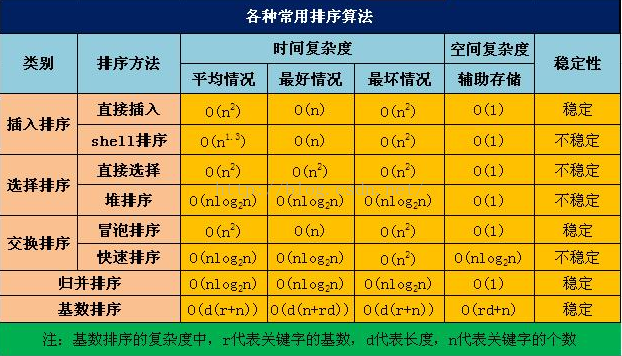
image

一些常见的排序算法的时间和空间复杂度，以及算法是否稳定：

image

时间复杂度

概念

时间复杂度是总运算次数表达式中受n的变化影响最大的那一项(不含系数)。

比如：一般总运算次数表达式类似于这样：

1
a*2n+b*n3+c*n2+d*n*lg(n)+e*n+f

当a!=0时，时间复杂度就是 O(2n);
当a=0,b<>0，时间复杂度就是 O(n3);
当a,b=0,c<>0，时间复杂度就是 O(n2);
依此类推。

例子:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
(1) // 循环了n*n次，当然是O(n2)
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            s++;
(2) // 循环了(n+n-1+n-2+...+1)≈(n2)/2，因为时间复杂度是不考虑系数的，所以也是O(n2)
    for(i=1;i<=n;i++)
        for(j=i;j<=n;j++)
            s++;
(3) // 循环了(1+2+3+...+n)≈(n^2)/2,当然也是O(n2)
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++)
            s++;
(4) // 循环了n-1≈n次，所以是O(n)
    i=1;k=0;
    while(i<=n-1) {
        k+=10*i;
        i++;
    }
(5) // 循环了(12+22+32+...+n2)=n(n+1)(2n+1)/6(这个公式要记住哦)≈(n3)/3，不考虑系数，自然是O(n3)
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++)
            for(k=1;k<=j;k++)
                x=x+1;

另外，在时间复杂度中，log2n与lg(n)(同lg10(n))是等价的，因为对数换底公式：
logab=logcb/logca
所以，log2n=log210 * lg(n),忽略掉系数，二者当然是等价的。

计算

1.一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。
但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。
并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2.一般情况下，算法的基本操作重复执行的次数是模块n的某一个函数f（n），
因此，算法的时间复杂度记做：T（n）=O（f（n））。随着模块n的增大，算法执行的时间的增长率和f（n）的增长率成正比，
所以f（n）越小，算法的时间复杂度越低，算法的效率越高。

在计算时间复杂度的时候，先找出算法的基本操作，然后根据相应的各语句确定它的执行次数，
再找出T（n）的同数量级（它的同数量级有以下：1，Log2n ，n ，nLog2n ，n的平方，n的三次方，2的n次方，n!），
找出后，f（n）=该数量级，若T(n)/f(n)求极限可得到一常数c，则时间复杂度T（n）=O（f（n））。

3.常见的时间复杂度
按数量级递增排列，常见的时间复杂度有：

常数阶O(1), 对数阶O(log2n), 线性阶O(n), 线性对数阶O(nlog2n), 平方阶O(n2)，立方阶O(n3)，…，k次方阶O(nk), 指数阶O(2n) 。

其中，
1）O(n)，O(n2)， 立方阶O(n3),…， k次方阶O(nk) 为多项式阶时间复杂度，分别称为一阶时间复杂度，二阶时间复杂度，依此类推。
2）O(2n)，指数阶时间复杂度，该种不实用
3）对数阶O(log2n)，线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高。

例：
算法：

1
2
3
4
5
6
7
8
9
10
for(i=1;i<=n;++i) {
    for(j=1;j<=n;++j) {
        // 该步骤属于基本操作 执行次数：n2
        c[i][j]=0;
        for(k=1;k<=n;++k) {
            //该步骤属于基本操作 执行次数：n3
            c[i][j]+=a[i][k]*b[k][j];
        }
    }
}

则有 T（n）= n2+n3，根据上面括号里的同数量级，我们可以确定 n3为T（n）的同数量级
则有f（n）= n3，然后根据T（n）/f（n）求极限可得到常数c
则该算法的 时间复杂度：T（n）=O（n3)

定义

如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)，它是n的某一函数 T(n)称为这一算法的“时间复杂性”。

当输入量n逐渐加大时，时间复杂性的极限情形称为算法的“渐近时间复杂性”。

我们常用大O表示法表示时间复杂性，注意它是某一个算法的时间复杂性。
大O表示只是说有上界，由定义如果f(n)=O(n)，那显然成立f(n)=O(n^2)，它给你一个上界，但并不是上确界，但人们在表示的时候一般都习惯表示前者。

此外，一个问题本身也有它的复杂性，如果某个算法的复杂性到达了这个问题复杂性的下界，那就称这样的算法是最佳算法。

“大O记法”：在这种描述中使用的基本参数是 n，即问题实例的规模，把复杂性或运行时间表达为n的函数。
这里的“O”表示量级 (order)，比如说“二分检索是 O(logn)的”,也就是说它需要“通过logn量级的步骤去检索一个规模为n的数组”。

记法 O(f(n)) 表示当n增大时，运行时间至多将以正比于 f(n)的速度增长。

这种渐进估计对算法的理论分析和大致比较是非常有价值的，但在实践中细节也可能造成差异。

例如，一个低附加代价的O(n2)算法在n较小的情况下可能比一个高附加代价的 O(nlogn)算法运行得更快。
当然，随着n足够大以后，具有较慢上升函数的算法必然工作得更快。

O(1)

交换i和j的内容

1
2
3
4
temp=i;i=j;j=temp;

解：以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。
算法的时间复杂度为常数阶，记作T(n)=O(1)。

如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。

O(n2)

1
2
3
4
5
6
sum=0；                 （1次）
for(i=1;i<=n;i++)       （n次）
for(j=1;j<=n;j++)       （n2次）
sum++；                 （n2次）

解：T(n)=2n^2+n+1=O(n^2) 该程序的时间复杂度T(n)=O(n2)。
1
2
3
4
5
6
7
8
9
10
for (i=1;i<n;i++) {
    // 频度是n-1
    y=y+1;
    for (j=0;j<=(2*n);j++) {
        //频度是(n-1)*(2n+1)=2n2-n-1 
        x++;
    }
}

解：f(n)=2n2-n-1+(n-1)=2n2-2 该程序的时间复杂度T(n)=O(n2)。

O(n)

1
2
3
4
5
6
7
8
9
10
// 频度:2
a=0;b=1;
// 频度:n
for (i=1;i<=n;i++) {
    s=a+b;　　　　// 频度:n-1
    b=a;　　　　　// 频度:n-1
    a=s;　　　　　// 频度:n-1
}

解：T(n)=2+n+3(n-1)=4n-1=O(n)。该程序的时间复杂度T(n)=O(n)。

O(log2n)

1
2
3
4
5
6
i=1;             // 频度是1
while (i<=n) {
    i=i*2;       // 频度是f(n)
}

解：2^f(n)<=n 即 f(n)<=log2n。该程序的时间复杂度T(n)，取最大值f(n)=log2n，T(n)=O(log2n)。

O(n3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(i=0;i<n;i++) {
    for(j=0;j<i;j++) {
        for(k=0;k<j;k++) {
            x=x+2;
        }
    }
}

解：
当 i=m,j=k 时, 内层循环的次数为 k。
当 i=m 时, j可以取 0,1,...,m-1。
所以这里最内循环共进行了 0+1+...+m-1=(m-1)m/2次。
进而,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6。
进而得出时间复杂度为 O(n3)。

我们还应该区分算法的最坏情况的行为和期望行为。

如快速排序的最坏情况运行时间是 O(n2)，但期望时间是 O(nlogn)。

通过每次都仔细地选择基准值，我们有可能把平方情况 (即O(n2)情况)的概率减小到几乎等于 0。

在实际中，精心实现的快速排序一般都能以 (O(nlogn)时间运行。

下面是一些常用的记法（技巧）：

访问数组中的元素是常数时间操作，或说O(1)操作。

一个算法如果能在每个步骤去掉一半数据元素，如二分检索，通常它就取 O(logn)时间。

用strcmp比较两个具有n个字符的串需要O(n)时间。

常规的矩阵乘算法是O(n3)，因为算出每个元素都需要将n对元素相乘并加到一起，所有元素的个数是n2。

指数时间算法通常来源于需要求出所有可能结果。例如，n个元素的集合共有2n个子集,所以要求出所有子集的算法将是O(2n)的。
指数算法一般说来是太复杂了，除非n的值非常小，因为，在这个问题中增加一个元素就导致运行时间加倍。

不幸的是，确实有许多问题 (如著名的“巡回售货员问题” )，到目前为止找到的算法都是指数的。
如果我们真的遇到这种情况，通常应该用寻找近似最佳结果的算法替代之。

空间复杂度

空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。

一个算法在计算机存储器上所占用的存储空间，包括程序代码所占用的空间，输入数据所占用的空间和辅助变量所占用的空间这三个方面。

算法的输入输出数据所占用的存储空间是由要解决的问题决定的，是通过参数表由调用函数传递而来的，它不随本算法的不同而改变。

存储算法本身所占用的存储空间与算法书写的长短成正比，要压缩这方面的存储空间，就必须编写出较短的算法。
算法在运行过程中临时占用的存储空间随算法的不同而异，有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地”进行的，是节省存储的算法，如这些介绍过的几个算法都是如此；

有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如将在第九章介绍的快速排序和归并排序算法就属于这种情况。

分析一个算法所占用的存储空间要从各方面综合考虑。

如对于递归算法来说，一般都比较简短，算法本身所占用的存储空间较少，但运行时需要一个附加堆栈，从而占用较多的临时工作单元；
若写成非递归算法，一般可能比较长，算法本身占用的存储空间较多，但运行时将可能需要较少的存储单元。

一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。

若一个算法为递归算法，其空间复杂度为递归所使用的堆栈空间的大小，它等于一次调用所分配的临时存储空间的大小乘以被调用的次数(即为递归调用的次数加1，这个1表不开始进行的一次非递归调用)。

算法的空间复杂度一般也以数量级的形式给出。

如当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；
当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为0(log2n)；
当一个算法的空间复杂度与n成线性比例关系时，可表示为0(n)。

若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；
若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。

对于一个算法，其时间复杂度和空间复杂度往往是相互影响的。

当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；
反之，当追求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。

另外，算法的所有性能之间都存在着或多或少的相互影响。

因此，当设计一个算法(特别是大型算法)时，要综合考虑算法的各项性能，算法的使用频率，算法处理的数据量的大小，算法描述语言的特性，算法运行的机器系统环境等各方面因素，才能够设计出比较好的算法。

空间复杂度是程序运行所以需要的额外消耗存储空间,也用O()来表示。

比如插入排序的时间复杂度是O(n2),空间复杂度是O(1)。
而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归都要存储返回信息。

一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。

算法执行时间的度量不是采用算法执行的绝对时间来计算的，因为一个算法在不同的机器上执行所花的时间不一样，在不同时刻也会由于计算机资源占用情况的不同，使得算法在同一台计算机上执行的时间也不一样，所以对于算法的时间复杂性，采用算法执行过程中其基本操作的执行次数，称为计算量来度量。

算法中基本操作的执行次数一般是与问题规模有关的，对于结点个数为n的数据处理问题，用T(n)表示算法基本操作的执行次数。

在评价算法的时间复杂性时，不考虑两算法执行次数之间的细小区别，而只关心算法的本质差别:

为此，引入一个所谓的O()记号，则T1(n)=2n=O(n),T2(n)=n+1=O(n)。

一个函数f(n)是O(g(n))的，则一定存在正常数c和m，使对所有的n>m，都满足f(n)<c*g(n)。

示例代码

示例代码（1）：

1
2
3
4
5
6
decimal Factorial(int n) {
    if (n == 0)
        return 1;
    else
        return n * Factorial(n - 1);
}

阶乘（factorial），给定规模 n，算法基本步骤执行的数量为 n，所以算法复杂度为 O(n)。

示例代码（2）：

1
2
3
4
5
6
7
8
9
int FindMaxElement(int[] array) {
    int max = array[0];
    for (int i = 0; i < array.Length; i++) {
        if (array[i] > max) {
            max = array[i];
        }
    }
    return max;
}

这里，n 为数组 array 的大小，则最坏情况下需要比较 n 次以得到最大值，所以算法复杂度为 O(n)。

示例代码（3）：

1
2
3
4
5
6
7
8
long FindInversions(int[] array) {
    long inversions = 0;
    for (int i = 0; i < array.Length; i++)
        for (int j = i + 1; j < array.Length; j++)
            if (array[i] > array[j])
                inversions++;
    return inversions;
}

这里，n 为数组 array 的大小，则基本步骤的执行数量约为 n*(n-1)/2，所以算法复杂度为 O(n2)。

示例代码（4）：

1
2
3
4
5
6
7
long SumMN(int n, int m) {
    long sum = 0;
    for (int x = 0; x < n; x++)
        for (int y = 0; y < m; y++)
            sum += x * y;
    return sum;
}

给定规模 n 和 m，则基本步骤的执行数量为 n*m，所以算法复杂度为 O(n2)。

示例代码（5）：

1
2
3
4
5
6
7
8
decimal Sum3(int n) {
    decimal sum = 0;
    for (int a = 0; a < n; a++)
        for (int b = 0; b < n; b++)
            for (int c = 0; c < n; c++)
                sum += a * b * c;
    return sum;
}

这里，给定规模 n，则基本步骤的执行数量约为 nnn ，所以算法复杂度为 O(n3)。

示例代码（6）：

1
2
3
4
5
6
decimal Calculation(int n) {
    decimal result = 0;
    for (int i = 0; i < (1 << n); i++)
        result += i;
    return result;
}

这里，给定规模 n，则基本步骤的执行数量为 2n，所以算法复杂度为 O(2n)。

示例代码（7）：

斐波那契数列：

Fib(0) = 0
Fib(1) = 1
Fib(n) = Fib(n-1) + Fib(n-2)
F() = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …

1
2
3
4
5
6
int Fibonacci(int n) {
    if (n <= 1)
        return n;
    else
        return Fibonacci(n - 1) + Fibonacci(n - 2);
}

这里，给定规模 n，计算 Fib(n) 所需的时间为计算 Fib(n-1) 的时间和计算 Fib(n-2) 的时间的和。

T(n<=1) = O(1)

T(n) = T(n-1) + T(n-2) + O(1)

1
2
3
4
5
6
                 fib(5)
             /             \
       fib(4)                fib(3)
     /      \                /     \
 fib(3)      fib(2)         fib(2)    fib(1)
/     \        /    \       /    \

通过使用递归树的结构描述可知算法复杂度为 O(2^n)。

示例代码（8）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int Fibonacci(int n) {
    if (n <= 1)
        return n;
    else {
        int[] f = new int[n + 1];
        f[0] = 0;
        f[1] = 1;

        for (int i = 2; i <= n; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }

        return f[n];
    }
}

同样是斐波那契数列，我们使用数组 f 来存储计算结果，这样算法复杂度优化为 O(n)。

示例代码（9）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int Fibonacci(int n) {
    if (n <= 1)
        return n;
    else
    {
        int iter1 = 0;
        int iter2 = 1;
        int f = 0;

        for (int i = 2; i <= n; i++) {
            f = iter1 + iter2;
            iter1 = iter2;
            iter2 = f;
        }

        return f;
    }
}

同样是斐波那契数列，由于实际只有前两个计算结果有用，我们可以使用中间变量来存储，这样就不用创建数组以节省空间。同样算法复杂度优化为 O(n)。

示例代码（10）：

通过使用矩阵乘方的算法来优化斐波那契数列算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
static int Fibonacci(int n) {
    if (n <= 1)
    return n;

    int[,] f = { { 1, 1 }, { 1, 0 } };
    Power(f, n - 1);

    return f[0, 0];
}

static void Power(int[,] f, int n) {
    if (n <= 1)
    return;

    int[,] m = { { 1, 1 }, { 1, 0 } };

    Power(f, n / 2);
    Multiply(f, f);

    if (n % 2 != 0)
    Multiply(f, m);
}

static void Multiply(int[,] f, int[,] m) {
    int x = f[0, 0] * m[0, 0] + f[0, 1] * m[1, 0];
    int y = f[0, 0] * m[0, 1] + f[0, 1] * m[1, 1];
    int z = f[1, 0] * m[0, 0] + f[1, 1] * m[1, 0];
    int w = f[1, 0] * m[0, 1] + f[1, 1] * m[1, 1];

    f[0, 0] = x;
    f[0, 1] = y;
    f[1, 0] = z;
    f[1, 1] = w;
}

优化之后算法复杂度为O(log2n)。

示例代码（11）：

在 C# 中使用公式法，得到更简洁的代码如下。

1
2
3
4
5
6
static double Fibonacci(int n) {
    double sqrt5 = Math.Sqrt(5);
    double phi = (1 + sqrt5) / 2.0;
    double fn = (Math.Pow(phi, n) - Math.Pow(1 - phi, n)) / sqrt5;
    return fn;
}

示例代码（12）：

1
2
3
4
5
6
7
8
9
10
11
12
13
private static void InsertionSortInPlace(int[] unsorted) {
    for (int i = 1; i < unsorted.Length; i++) {
        if (unsorted[i - 1] > unsorted[i]) {
            int key = unsorted[i];
            int j = i;
            while (j > 0 && unsorted[j - 1] > key) {
                unsorted[j] = unsorted[j - 1];
                j--;
            }
            unsorted[j] = key;
        }
    }
}

插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的有序数据。算法适用于少量数据的排序，时间复杂度为 O(n2)。

推导案例

摘自软考书。

已知递推关系式T(n)=2T(n/2)+n，求时间复杂度。

这个递推关系式其实是在给n个元素进行快速排序时最好情况（每次分割都恰好将记录分为两个长度相等的子序列）下的时间递推关系式，其中T(n/2)是一个子表需要的处理时间，n 为当次分割需要的时间。

注意，这里实际上是用比较次数（数组的比较）来度量表示所需时间。

可以对此表达式进行变形得：
T(n)/n-T(n/2)/(n/2)=1

用n/2代替上式中的n可得：
T(n/2)/(n/2)-T(n/4)/(n/4)=1

继续用n/2代替上式中的n可得：
T(n/4)/(n/4)-T(n/8)/(n/8)=1
…
T(2)/2-T(1)/1=1

算法共需要进行[lbn]+1次分割(n个元素的序列的对半分割树的高度跟具有n个结的完全二叉树高度相等，软设级别的只需知道即可，不必深究)。

将上述[lbn]+1个式子相加，删除相互抵消的部分得：
T(n)/n-T(1)/1=[lbn]+1

而T(1)=1，那么上式可转化为：
T(n)=n[lbn]+2n

而在求时间复杂度时关注“大头”，注意到O(n)<O(nlbn)而且对数的底可省略或为任意常数值，那么：

T(n)=O(nlogn)=O(nlgn)

数学上，一般将底为10的对数简略为lg，底为2的对数简略为lb，底为e的对数简略为ln。

参考博文

1
2
3