常见的数组排序算法(Java版)
在一些项目中经常会使用排序算法,Java的API中也有各种已经提供好的排序算法,比如TreeSet的sort方法。在会使用这些即有算法的同时,自己也加以学习整理出常见的排序算法(均为升序排序)。
常见的排序算法:
插入排序,选择排序,冒泡排序,希尔排序,快速排序,交换元素等
推荐一个常见算法的动态演示网站:https://visualgo.net/
文中插图来自网络。
常见的排序算法
交换元素
在写排序算法之前,先说一下交换元素的方法。交换数组中两个元素主要有三种做法:中间变量法,异或法,加减法。其中,异或法和加减法更适用于整型(包括长整型),中间变量法则是万能交换元素的方法。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52/**
* 异或方式交换元素,没有中间变量,不会增加数值长度
*
* @param n
* 要交换元素的数组
* @param i
* 第一个交换元素的数组下标
* @param j
* 第二个交换元素的数组小标
*/
public static void swap(int[] n, int i, int j) {
checkSwapArgs(n, i, j);
n[i] ^= n[j];
n[j] ^= n[i];
n[i] ^= n[j];
}
/**
*
* 加减方式交换元素,注意可能带来的数据溢出和符号位问题
*
* @param n
* 要交换元素的数组
* @param i
* 第一个交换元素的数组下标
* @param j
* 第二个交换元素的数组小标
*/
private static void swap2(int[] n, int i, int j) {
checkSwapArgs(n, i, j);
n[i] = n[i] + n[j];
n[j] = n[i] - n[j];
n[i] = n[i] - n[j];
}
/**
*
* 中间变量法,方法简单,带来额外的内存开销,不过开销很小
*
* @param n
* 要交换元素的数组
* @param i
* 第一个交换元素的数组下标
* @param j
* 第二个交换元素的数组小标
*/
private static void swap3(int[] n, int i, int j) {
checkSwapArgs(n, i, j);
int t = n[i];
n[i] = n[j];
n[j] = t;
}
冒泡排序
冒泡排序就像水中冒泡一样,每次遍历中都将本次遍历中最大的元素排在最后(上)面。这里的冒泡算法做了一些小优化,如果在排序中,已经出现了数组排序好的情况则停止排序。在学习排序算法的时候也找到一写算法的动图,这里粘贴一下。
1 | /** |
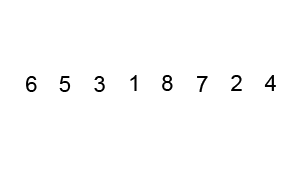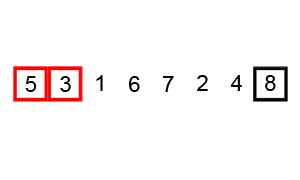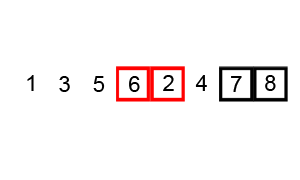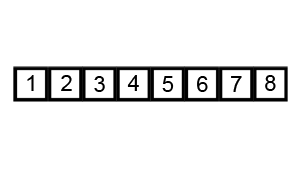
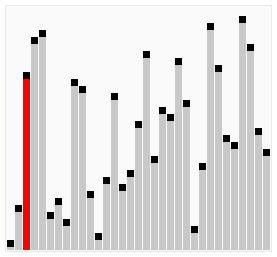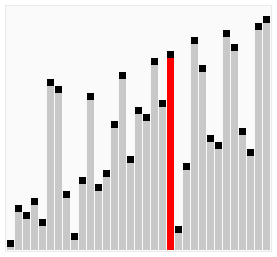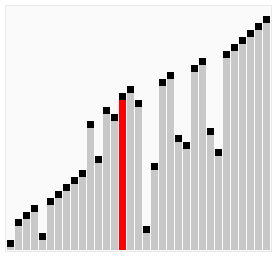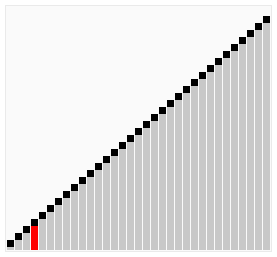
这个算法的名字由来是因为越小(或越大)的元素会经由交换慢慢“浮”到数列的顶端。
选择排序
选择排序,是指在每次排序中,在尚未排序的序列中选择一个最小的然后接到已经排序好的算法后面。
1 | /** |
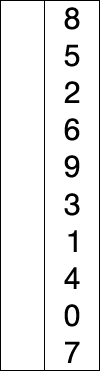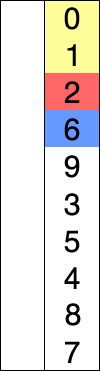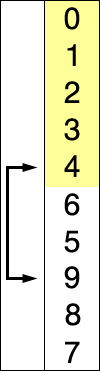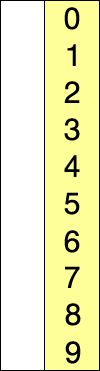


插入排序
插入排序和选择排序有类似的地方,插入排序是每次从尚未排序的剩余序列中取第一个,然后按照其他如冒泡排序等方法插入到前面已经排序好的序列中。
注意是从已经排序好的序列最后一个开始,倒过来找到合适的位置后插入。
1 | /** |



插入排序不会动右边的元素,选择排序不会动左边的元素;由于插入排序涉及到的未触及的元素要比插入的元素要少,涉及到的比较操作平均要比选择排序少一半。
希尔排序
希尔排序开始时设定一个gap(初始时设置为数组的长度),然后像跳格子一样,等间隔(gap)的取出序列中的数,在对取出的数进行冒泡选择插入排序。每次循环gap减半,逐步细化间隔。
希尔排序,也叫递减增量排序,是插入排序的一种更高效的改进版本。希尔排序是不稳定的排序算法。
1 | /** |


希尔排序是基于插入排序的以下两点性质而提出改进方法的:
1) 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
2) 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n^2)的排序(冒泡排序或直接插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
快速排序
快速排序是一个不稳定算法。原理形象的说,就是每次递归时,在该序列段内选择一个数(一般为第一个数)做为基准,然后将这个序列中比这个数大的数放在右边,比它小的放在左边。
Java的API中可以使用深度优化的Arrays.sort()方法。对于基础类型,底层使用快速排序。对于非基础类型,底层使用归并排序。
1 | /** |


对一般快速排序进行一些改进可以提高其效率。
- 当划分到较小的子序列时,通常可以使用插入排序替代快速排序。
- 三平均分区法(Median of three partitioning)。
由于快速排序在排序算法中具有排序速度快,而且是就地排序等优点,使得在许多编程语言的内部元素非稳定的排序实现中采用的就是快速排序。
可以参考这篇博客
其他排序
其他的排序方法还有:
归并排序
采用“分治”思想,简单将就是分块执行,每部分排序好后,再逐层合并结果。
堆排序
堆排序的存储元素的数据结构为树,并且满足堆的性质(完全二叉树)。
排序算法的性能
常用的排序算法的时间复杂度和空间复杂度
| 排序法 | 最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | O($n^{2}$) | O($n^{2}$) | 稳定 | O(1) |
| 快速排序 | O($n^{2}$) | O($n*\log_2n$) | 不稳定 | O($\log_2n$)~O(n) |
| 选择排序 | O($n^{2}$) | O($n^{2}$) | 稳定 | O(1) |
| 二叉树排序 | O($n^{2}$) | O($n*\log_2n$) | 不稳定 | O(n) |
| 插入排序 | O($n^{2}$) | O($n^{2}$) | 稳定 | O(1) |
| 堆排序 | O($n*\log_2n$) | O($n*\log_2n$) | 不稳定 | O(1) |
| 希尔排序 | O | O | 不稳定 | O(1) |
结果测试
只是验证了排序算法的正确性,没有对性能等进行测试。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56public void test() {
int a[] = RandomIntegerArrayMethod.randomSelectArray(0, 9, 10);
TestMethod.print(a);
int b[] = a.clone();
swap(b, 3, 6);
TestMethod.print(b);
swap2(b, 1, 4);
TestMethod.print(b);
swap3(b, 5, 2);
TestMethod.print(b);
int c1[] = a.clone();
insertSort(c1);
TestMethod.print(c1);
int c2[] = a.clone();
bubbleSort(c2);
TestMethod.print(c2);
int c3[] = a.clone();
selectSort(c3);
TestMethod.print(c3);
int c4[] = a.clone();
shellSort(c4);
TestMethod.print(c4);
int c5[] = a.clone();
quickSort(c5);
TestMethod.print(c5);
// other test
int d[] = { 2, 4, 5, 6, 2, 0, 2 };
int d1[] = d.clone();
insertSort(d1);
TestMethod.print(d1);
int d2[] = d.clone();
bubbleSort(d2);
TestMethod.print(d2);
int d3[] = d.clone();
selectSort(d3);
TestMethod.print(d3);
int d4[] = d.clone();
shellSort(d4);
TestMethod.print(d4);
int d5[] = d.clone();
quickSort(d5);
TestMethod.print(d5);
// insertSort(null);
}
测试结果
6 9 8 7 2 4 0 3 1 5
6 9 8 0 2 4 7 3 1 5
6 2 8 0 9 4 7 3 1 5
6 2 4 0 9 8 7 3 1 5
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 2 2 2 4 5 6
0 2 2 2 4 5 6
0 2 2 2 4 5 6
0 2 2 2 4 5 6
0 2 2 2 4 5 6